Question 201190: Hey guys and girls, I have a bit of a problem here I have 50 home work questions that I have to submit by mid-night and I'm in a bit over my head at this point with both my summer classes and there finals tonight and tomorrow. If any body can help me with a few of these problems I would be very, very greatfull!I have to solve the follwing A,{Y=^X2+4X-5 & Y=-X^2+12X-11] B, {X^2+Y^=193 &X-Y=5} C, {X*Y=45 & 3X-Y=-6} D,{X*Y=8 & X^2+Y^2=65} E, {X+Y=-8 & (X-2)^2+(Y+7)^2=5}
I know this is not normal but I have to be at school to take one of my finals and I,m not too good at the substitution method these questions would probabley take me 2 hours to get the correct solutions not to mention the other 46 problems I have to solve! So if anybody is generous enough to help me with these solutions THANK YOU!!! fyi summer sessions are horrible....
Found 2 solutions by jim_thompson5910, Alan3354:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Ok I would love to help you with all of these, but it would take me way too long (you'll see below). So I'm only going to do the first two to get you started.
A)
 Start with the first equation. Start with the first equation.
 Plug in Plug in 
 Get all terms to the left side. Get all terms to the left side.
 Combine like terms. Combine like terms.
Notice that the quadratic 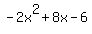 is in the form of is in the form of  where where  , ,  , and , and 
Let's use the quadratic formula to solve for "x":
 Start with the quadratic formula Start with the quadratic formula
 Plug in Plug in  , ,  , and , and 
 Square Square  to get to get  . .
 Multiply Multiply 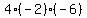 to get to get 
 Subtract Subtract  from from  to get to get 
 Multiply Multiply  and and  to get to get  . .
 Take the square root of Take the square root of  to get to get  . .
 or or  Break up the expression. Break up the expression.
 or or  Combine like terms. Combine like terms.
 or or  Simplify. Simplify.
So the solutions for "x" are  or or 
-----------------------------------------------------------
Let's find the value of "y" when 
 Go back to the first equation. Go back to the first equation.
 Plug in Plug in 
 Square 1 to get 1 Square 1 to get 1
 Multiply Multiply
 Combine like terms. Combine like terms.
So when  , ,  giving the ordered pair (1,0) giving the ordered pair (1,0)
--------------
Let's find the value of "y" when 
 Go back to the first equation. Go back to the first equation.
 Plug in Plug in 
 Square 3 to get 9 Square 3 to get 9
 Multiply Multiply
 Combine like terms. Combine like terms.
So when  , ,  giving the ordered pair (3, 16) giving the ordered pair (3, 16)
=======================================================================
Answer:
So the 2 ordered pair solutions are:
(1,0) and (3,16)
B)
 Start with the second equation. Start with the second equation.
 Add "y" to both sides. Add "y" to both sides.
 Move onto the second equation. Move onto the second equation.
 Plug in Plug in 
 FOIL FOIL
 Subtract 193 from both sides. Subtract 193 from both sides.
 Combine like terms. Combine like terms.
Notice that the quadratic 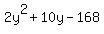 is in the form of is in the form of 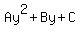 where where  , ,  , and , and 
Let's use the quadratic formula to solve for "y":
 Start with the quadratic formula Start with the quadratic formula
 Plug in Plug in  , ,  , and , and 
 Square Square  to get to get  . .
 Multiply Multiply 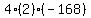 to get to get 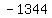
 Rewrite Rewrite 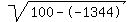 as as 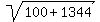
 Add Add  to to  to get to get 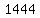
 Multiply Multiply  and and  to get to get  . .
 Take the square root of Take the square root of 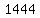 to get to get  . .
 or or  Break up the expression. Break up the expression.
 or or  Combine like terms. Combine like terms.
 or or  Simplify. Simplify.
So the solutions (for "y") are  or or 
------------------------------------------------------------
Let's find the value of "x" when 
 Go back to the previously isolated equation Go back to the previously isolated equation
 Plug in Plug in 
 Add Add
So when  , ,  . This means that we have the ordered pair (12, 7) . This means that we have the ordered pair (12, 7)
-----------------------------
Let's find the value of "x" when 
 Go back to the previously isolated equation Go back to the previously isolated equation
 Plug in Plug in 
 Subtract Subtract
So when  , ,  . This means that we have the ordered pair (-7, -12) . This means that we have the ordered pair (-7, -12)
=======================================================================
Answer:
So the 2 ordered pair solutions are:
(12, 7) and (-7, -12)
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! A,{Y=^X2+4X-5 & Y=-X^2+12X-11
I assume you want to find the values of x common to these 2 eqns, where they intersect.
Since they both = y, they equal each other.
X^2+4X-5 = -X^2+12X-11
2x^2 - 8x + 6 = 0
(2x - 2)*(x - 3) = 0
x = 3
x = 1
-------
x = 3 --> y = 16 gives the point (3,16)
x = 1 --> y = 0 gives the point (1,0)
These are the 2 points of intersection of the 2 functions.
------------------------
B, X^2+Y^2=193 &X-Y=5
x = y+5
(y+5)^2 + y^2 = 193
y^2 + 10y + 25 + y^2 = 193
2y^2 + 10y - 168 = 0
y^2 - 5y - 84 = 0
(y-12)*(y+7) = 0
y = -7
y = 12
Sub and solve for x as in the 1st one.
--------------------------------------
C X*Y=45 & 3X-Y=-6
y = 3x+6
x*(3x+6) = 45
x^2 + 2x - 15 = 0
(x+5)*(x-3) = 0
x = 3
x = -5
------------
D X*Y=8 & X^2+Y^2=65
Similar to B but with 4 points of intersection.
---------------
E X+Y=-8 & (X-2)^2+(Y+7)^2=5
More of the same
email me via the thank you note if you want me to check your work.
|
|
|