Question 172376: a cyclist, riding at 21 miles per hour, leaves town. Four hours later, another cyclist leaves from the same starting point, traveling in the same direction at an average of 33 miles per hour. how long did it take the second cyclist to catch up to the first cyclist?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! a cyclist, riding at 21 miles per hour, leaves town. Four hours later,
another cyclist leaves from the same starting point, traveling in the
same direction at an average of 33 miles per hour.
:
how long did it take the second cyclist to catch up to the first cyclist?
;
Let t = 2nd cyclist travel time
then
(t+4) = 1st cyclist travel time
:
When the 2nd cyclists catches the 1st, they will have traveled the same distance
Write distance equation from this fact: Dist = speed * time
:
2nd cyclist dist = 1st cyclist dist
;
33t = 21(t+4)
33t = 21t + 84
33t - 21t = 84
12t = 84
t = 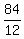
t = 7 hrs, for the 2nd cyclist to catch the 1st
;
:
Check solution by finding the dist traveled by each:
11*21 = 231 mi
7*33 = 231 mi; confirms our solution
|
|
|