SOLUTION: i have some problems with this system ? can you tell me how to solution sytem sytem is x^3 + y^3 = 1 x^2y + 2xy^2 + Y^3 = 2 please contact with me as soon as you ca

Let 









Now we can solve each for  as long as we require that
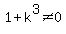 and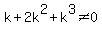 

So we will take Case 1 as when they are both true:

Case 1: 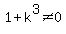  and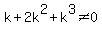 

Then we can solve both for  without
dividing by 0:



Since the left sides are equal, so are the right 
sides:



Cross multiply:





Get 0 on the right and left side in descending
order:



Factor k^2 out of the first two terms on the left,
and factor -1 out of the last two terms on the left:



Factor 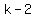 out of both terms on the left:



Factor the second parentheses on the left:



Using the zero-factor principle:

 

Remember that the requirements for Case 1 were:

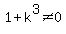 and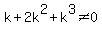 

We investigate to see whether  satisfies
both of those requirements. Substituting,

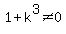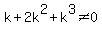
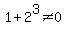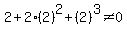
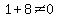 and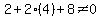 
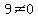 and 
 and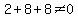 
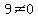 and 
 and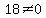 

So there are both satisfied, so we can use 

We now investigate to see whether  satisfies
both of those requirements. Substituting,

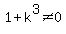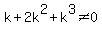
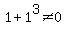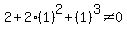
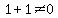 and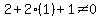 
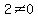 and 
 and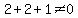 
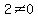 and 
 and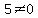 

So these are both satisfied, so we can also use 

We now investigate to see whether  satisfies
both of those requirements. Substituting,

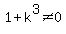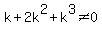
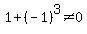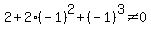
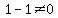 and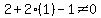 
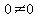 and 
 and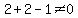 
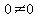 and 
 and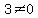 

Since the first is not satisfied we cannot use 

Now we use and since ,  in the original:






solving both for 



So these are the same, so we can

get the real solution by taking cube roots
of both sides:



rationalizing:







And since in this case 

we have solution

 

But that's not necessarily the only solution.

Now we use and since ,  in the original:








solving both for 



So these are the same, so we can
get a real solution by taking cube roots
of both sides:



rationalizing:







And since in this case 

we have solution

 

So we have found two solutions.  But this
was only for Case 1, when 

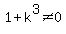 and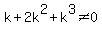 

We must investigate the possibility of
solutions when one or both of these are
violated:

Case 2: 

This means that

 or 

Now we use and since ,  in the original:






This is certainly not true, so Case 2
 is not possible since it produces
no solutions.

Case 3: 

Factoring out k on the left:



Factoring the trinomial in parenheses:



Using the zero-factor principle:



We have already seen that  is not
possible, so we only need investigate 

Now we use and since ,  in the original:






This is certainly not true, so Case 3
 is not possible since it produces
no solutions.

So the only real solutions are:



and

 

However, there are also some imaginary solutions.  I did not
find those. They would require finding the 2 imaginary
cube roots each of 4 and 3.  I only considered the real
cube roots of 4 and 3.  Post again if you want all the
imaginary solutions as well.

Edwin