Question 166691: Please help with the following equation:
A medical supply company has 1150 worker-hours for production, maintenance, and inspection. Using this and other factors, the number of hours used for each operation, P, M, and I, respectively, is found by solving the following system of equations. Find P, M and I.
P + M + I = 1150
P = 4I - 100
P = 6M + 50
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A medical supply company has 1150 worker-hours for production, maintenance, and inspection. Using this and other factors, the number of hours used for each operation, P, M, and I, respectively, is found by solving the following system of equations. Find P, M and I.
P + M + I = 1150
P = 4I - 100
P = 6M + 50
:
Using the 1st two equations, rearrange the 2nd to have:
P + M + I = 1150
P + 0 -4I = -100
-------------------subtraction eliminates P
M + 5I = 1250
:
Using the 1st and 3rd equation, rearrange the 3rd to have:
P + M + I = 1150
P -6M + 0 = 50
-------------------Subtraction eliminate P
+7M + I = 1100
:
Multiply the above equation by 5, subtract M + 5I = 1250 from it:
35M + 5I = 5500
M + 5I = 1250
---------------------Subtraction eliminates I, find M
34M = 4250
M = 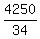
M = 125 hrs of maint
:
Using M + 5I = 1250, Find I
125 + 5I = 1250
5I = 1250 - 125
I = 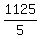
:
I = 225 hrs of inspection
:
Use P = 6M + 50 to find P
P = 6(125) + 50
P = 750 + 50
P = 800 hrs production
:
Confirm solutions in the 1st equation
800 + 125 + 225 = 1150
|
|
|