SOLUTION: Identify the axis of symmetry, create a suitable table of values, then sketch the graph (including the axis of symmetry). y = –x² + 3x – 3

First make the table:

x|-1| 0| 1| 2| 3| 4
y|-7|-3|-1|-1|-3|-7

Then we'll plot those points



Next we'll calculate the axis of symmetry:

Rule:
The axis of syymetry of the graph whose equation is

y = Ax² + Bx + C

is the vertical line whose equation is 

x =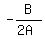 

You may not have learned about the vertex, but I'll
throw that in too.

Rule:
The vertex is the point

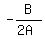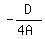(, ), where D = B²-4AC

(D is called the "discriminant")

So in the case of 

y = –x² + 3x – 3

A = -1, B = 3, C = -3 

so the axis of symmetry is the vertical line
whose equation is

x =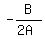 

or

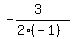x =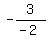 

x = 

x = 

So we'll sketch in the
axis of symmetry:



and to find the vertex,

D = B² - 4AC
D = 3² - 4(-1)(-3)
D = 9 - 12
D = -3

So the vertex is the point

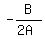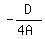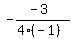(,  or

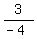(, , or

(, , or

(, ),  

So we'll plot the vertex point too:



Now we'll sketch in the graph, which is
a parabola:

  

Edwin