Question 1210378: Find all ordered pairs x, y of real numbers such that x+y=10 and x^3+y^3=300.
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3816)   (Show Source):
You can put this solution on YOUR website!
x+y = 10
(x+y)^3 = 10^3
x^3+3x^2y+3xy^2+y^3 = 1000 .......... binomial theorem
(x^3+y^3) + (3x^2y+3xy^2) = 1000
(x^3+y^3) + 3xy(x+y) = 1000
300+3xy(10) = 1000 ............. plug in x+y=10 and x^3+y^3=300
300+30xy = 1000
30xy = 1000-300
30xy = 700
xy = 700/30
xy = 70/3
x+y = 10
x(x+y) = 10x ...... multiplying both sides by x
x^2+xy = 10x
x^2+70/3 = 10x ........... plug in xy = 70/3 found earlier
3x^2+70 = 30x ........... multiply both sides by the LCD 3
3x^2-30x+70 = 0
I'll let the student finish up.
I recommend using the quadratic formula.
You should get two distinct real number solutions for x.
Once determining x, you can determine the paired value of y.
Due to symmetry, if (a,b) is a solution then (b,a) is the other solution.
Answer by ikleyn(52778)  (Show Source):
You can put this solution on YOUR website! .
Find all ordered pairs x, y of real numbers such that x+y=10 and x^3+y^3=300.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Your starting equations are
x + y = 10, (1)
x^3 + y^3 = 300. (2)
In equation (2), use the decomposition of the sum of cubes in the left side
x^3 + y^3 = (x+y)*(x^2 - xy + y^2).
In this decomposition, replace the factor (x+y) by 10, based on equation (1).
You will get then
x^2 - xy + y^3 = 30. (3) (after dividing both sides by 10)
So, now you have equivalent system of equations
x + y = 10, (4)
x^2 - xy + y^2 = 30, (5)
but the degree is lowered from 3 to 2, which is good.
Now, from equation (4) express y = 10-x and substitute it into equation (5). You will get
x^2 - x(10-x) + (10-x)^2 = 30,
x^2 - 10x + x^2 + 100 - 20x + x^2 = 30,
3x^2 - 30x + 70 = 0.
Use the quadratic formula
 =  =  =  .
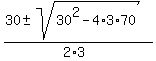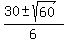Two values for x are  = 6.290994449 (approximately) and  = 3.709005551 (approximately).
The ordered pairs are (x,y) = (  ,  ) = (  , )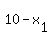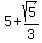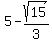
and (x,y) = (  ,  ) = (  , ).
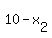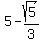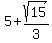You may check that 6.290994449^3 + 3.709005551^3 = 300.0000000205... , so the approximate solution is very good.
You also may check that exact solutions (x,y) satisfy equations (1) and (2) precisely.
Solved.
|
|
|
