Question 1209168: Find all ordered pairs (x,y) of real numbers such that x + y = 10 and x^2 + y^2 = 62 + 2xy.
For example, to enter the solutions (2,4) and (-3,9), you would enter "(2,4),(-3,9)" (without the quotation marks).
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13258)   (Show Source): (Show Source):
You can put this solution on YOUR website!


Whenever the given equations have terms of  , ,  , and , and  , one thing you want to look at is using one of these: , one thing you want to look at is using one of these:


For this problem....



Solve the first given equation for y in terms of x and substitute in this last equation.





That quadratic does not factor, so use the quadratic formula to find
 and and 
Partially simplified, those roots are
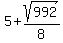 and and 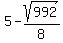
The given equations are symmetrical in x and y, so the two solutions are that x and y are equal to, in either order, 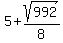 and and 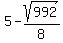
Those numbers, confirmed by graphing the system of equations using desmos.com, are approximately 8.937 and 1.063.
ANSWERS (approximately): (8.937,1.603) and (1.063,8.937)
Answer by ikleyn(53419)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I will re-formulate the problem in normal human mathematical language,
throwing out all unnecessary words
Find all real solutions to this system of equations
x + y = 10 (1)
x^2 + y^2 = 62 + 2xy. (2)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Transform second equation this way
x^2 - 2xy + y^2 = 62,
(x-y)^2 = 62,
|x-y| = 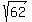 .
Then the given system of equations takes the form
x + y = 10,
x - y = +/- .
Then the given system of equations takes the form
x + y = 10,
x - y = +/- 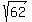 .
It falls apart in two systems of equations. First system is
x + y = 10,
x - y = .
It falls apart in two systems of equations. First system is
x + y = 10,
x - y = 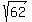 .
By adding equations, you will get
2x = 10 + .
By adding equations, you will get
2x = 10 + 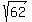 ---> x = 5 + ---> x = 5 + 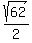 ,
By subtracting equations, you will get
2y = 10 - ,
By subtracting equations, you will get
2y = 10 - 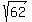 ---> y = 5 - ---> y = 5 - 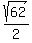 .
Second system of equations is
x + y = 10,
x - y = .
Second system of equations is
x + y = 10,
x - y = 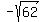 .
By adding equations, you will get
2x = 10 - .
By adding equations, you will get
2x = 10 - 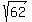 ---> x = 5 - ---> x = 5 - 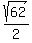 ,
By subtracting equations, you will get
2y = 10 + ,
By subtracting equations, you will get
2y = 10 + 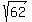 ---> y = 5 + ---> y = 5 + 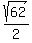 .
ANSWER. There are two solutions: (x,y) = ( .
ANSWER. There are two solutions: (x,y) = (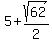 , ,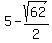 )
and (x,y) = ( )
and (x,y) = (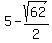 , ,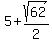 ). ).
Solved.
|
|
|