Question 1206248: what would the graph of an exponential function with range y<1,y∈R and a y-intercept of 0 look like. And what are the domain, horizontal asymptote, x-intercept.
Found 4 solutions by Edwin McCravy, ikleyn, mccravyedwin, math_tutor2020:
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The goal of this my post is twofold.
First is to make a correction in Edwin's post.
Second is to expand it and to show another examples of similar functions.
In his post, Edwin, actually, found a function y = 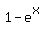 , satisfying the imposed conditions , satisfying the imposed conditions
 But he mistakenly wrote it as y =
But he mistakenly wrote it as y = 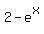 .
Here "2" is a mistake or a typo. The correct formula for the function is y = .
Here "2" is a mistake or a typo. The correct formula for the function is y = 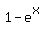 .
Its domain is .
Its domain is 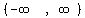 .
Its horizontal asymptote is .
Its horizontal asymptote is  .
Its x-intercept (and its y-intercept) is (0,0).
Actually, there are infinitely many of such functions, satisfying the imposed conditions.
They are of the form y = .
Its x-intercept (and its y-intercept) is (0,0).
Actually, there are infinitely many of such functions, satisfying the imposed conditions.
They are of the form y = 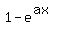 , with positive real coefficient "a" in the exponent. , with positive real coefficient "a" in the exponent.
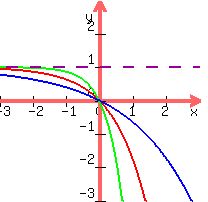 In this plot, red curve is for a = 1; green curve is for a = 2 and blue curve is for a = 0.5.
Their domain is
In this plot, red curve is for a = 1; green curve is for a = 2 and blue curve is for a = 0.5.
Their domain is 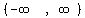 .
Their horizontal asymptote is .
Their horizontal asymptote is  .
Their x-intercept (and their y-intercept) is (0,0).
There are solutions of another form.
They are of the form y = .
Their x-intercept (and their y-intercept) is (0,0).
There are solutions of another form.
They are of the form y = 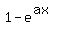 , with NEGATIVE real coefficient "a" in the exponent.
They also satisfy all imposed conditions.
See the plots below , with NEGATIVE real coefficient "a" in the exponent.
They also satisfy all imposed conditions.
See the plots below
 In this plot, red curve is for a = -1; green curve is for a = -2 and blue curve is for a = -0.5.
Their domain is the same
In this plot, red curve is for a = -1; green curve is for a = -2 and blue curve is for a = -0.5.
Their domain is the same 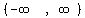 .
Their horizontal asymptote is .
Their horizontal asymptote is  .
Their x-intercept (and their y-intercept) is (0,0). .
Their x-intercept (and their y-intercept) is (0,0).
Solved.
Answer by mccravyedwin(406)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Ikleyn is right that I typed 2 for 1, but I could not have
shown the graph with 2 in there using the site's notation
for graphing. You'll notice I did correct the typo above.
Also the request was for the graph of AN exponential
function, not THE ONE AND ONLY possible one.
There is such a thing as over-teaching by over-
generalizing. Students who post on here are
struggling with their math class, not doing
mathematical research. Sometimes I think some
tutors on here are not trying to teach students,
but instead, putting on a show to "say without
saying" to other tutors, "Look how clever I am!
-- (and how unclever you are!)"
Edwin
Answer by math_tutor2020(3816)   (Show Source): (Show Source):
|
|
|