Question 1204796: In his motorboat, Tran travels upstream at top speed to his favorite fishing spot, a distance of 6 miles, in 2 hours. Returning, he finds that the trip downstream, still at top speed, takes only 1.5 hours. Find the speed of Tran's boat and the speed of the current.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
In his motorboat, Tran travels upstream at top speed to his favorite fishing spot,
a distance of 6 miles, in 2 hours. Returning, he finds that the trip downstream,
still at top speed, takes only 1.5 hours. Find the speed of Tran's boat and the speed of the current.
~~~~~~~~~~~~~~~~~~~
Let x be the speed of Tran's boat in sill water,
and let c be the speed of the current.
Then we have these equations
u + c = 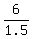 = 4 (1) for the speed traveling downstream
u - c = 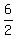 = 3 (2) for the speed traveling upstream
Add this equations. You will get
2u = 4 + 3 = 7 ---> u = 7/2 = 3.5 miles per hour.
Now from equation (1)
c = 4 - u = 4 - 3.5 = 0.5 miles per hour.
ANSWER. The speed of Tran's boat in still water is 3.5 miles per hour.
The speed of the current is 0.5 miles per hour.
Solved.
----------------
It is a typical and standard Upstream and Downstream round trip word problem.
You can find many similar fully solved problems on upstream and downstream round trips with detailed solutions in lessons
- Wind and Current problems
- More problems on upstream and downstream round trips
in this site, where you will find other similar solved problems with detailed explanations.
Read them attentively and learn how to solve this type of problems once and for all.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Upstream, the rate is 6/2 = 3mph; downstream, it is 6/1.5 = 4mph.
This "upstream, downstream" problem is a very common type of problem in which the sum of two numbers is A and the difference of those two numbers is B; in this problem those numbers are 4 and 3.
If formal algebra is not required, this kind of problem is easily solved using logical reasoning.
The boat speed, plus the current speed, is 4mph; the boat speed, minus the current speed, is 3mph.
Picture those numbers on a number line. When you start with the boat speed and add the current speed, the result is 4mph; when you start with the boat speed and subtract the current speed, the result is 3mph.
Logic then tells you that the boat speed is halfway between 3mph and 4mph -- i.e., 3.5mph. And then that means the current speed is 0.5mph.
ANSWERS: Boat speed 3.5mph; current speed 0.5mph
In general, for any problem like this...
If A+B = m and A-B = n,
Then A is halfway between m and n (i.e., the average of m and n) and B is the difference between that average and either of m or n.
|
|
|
