Question 1203513: A large multiplex movie house has many theaters. The largest theater has 46 rows. There are 16 seats in the first row. Each row has two seats more than the previous row. How many total seats are there in this​ theater?
Found 4 solutions by josgarithmetic, math_tutor2020, greenestamps, ikleyn:
Answer by josgarithmetic(39617)   (Show Source):
Answer by math_tutor2020(3816) (Show Source):
You can put this solution on YOUR website!
Answer: 2806
Work Shown
a1 = first term = 16
d = common difference = 2
Sn = sum of the first n terms of an arithmetic sequence
Sn = (n/2)*(2*a1 + d*(n-1))
Sn = (n/2)*(2*16 + 2*(n-1))
S46 = (46/2)*(2*16 + 2*(46-1))
S46 = 2806
Or we can compute the sum a slightly different way.
an = nth term of arithmetic sequence
an = a1 + d*(n-1)
an = 16 + 2*(n-1)
a46 = 16 + 2*(46-1)
a46 = 106
There are 106 seats in the 46th row.
Sn = sum of the first n terms of an arithmetic sequence
Sn = (n/2)*(first term + nth term)
Sn = (n/2)*(a1 + an)
S46 = (46/2)*(a1 + a46)
S46 = (46/2)*(16 + 106)
S46 = 2806
The sum of the first 46 terms of the arithmetic sequence {16,18,20,22,...} is 2806 which is the total number of seats in the theater room.
Spreadsheet software can be used to confirm the answer.
Various online calculators are helpful as well.
A longer way to confirm the answer would be to compute the sum
16+18+20+22+24+26+28+30+32+34+36+38+40+42+44+46+48+50+52+54+56+58+60+62+64+66+68+70+72+74+76+78+80+82+84+86+88+90+92+94+96+98+100+102+104+106 = 2806
But it would be pointless busy-work to type all of that into a calculator.
I do not recommend this confirmation method. Stick to the spreadsheet or other specialized calculators.
Answer by greenestamps(13198)  (Show Source):
You can put this solution on YOUR website!
The response from one tutor simply says "find the formula and use it". That is fine if all you want to do is complete the assignment and not learn anything about how to solve problems like this.
The response from the other tutor shows how to calculate the answer using either of two formulas that are commonly found in textbooks or other references. But using those formulas doesn't really teach you how to find the answer, because it is not clear WHY the formulas work.
It's always nice, when you are using a formula to find the answer to a problem, to be able to see WHY the formula works.
So let's look at the two formulas shown in that response; then we will look at a slight variation that makes it clear WHY the formula works.
The first formula commonly found in textbooks is this:
where n is the number of terms, a(1) is the first term, and d is the common difference.
That formula is valid -- but looking at it doesn't give you a clear understanding of why.
With first term a(1) and common difference d, the n-th term is 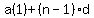 (first term plus the common difference (n-1) times); so the expression 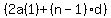 in the formula is the sum of the first and last terms.
That makes this formula equivalent to the other formula shown in the response from the other tutor: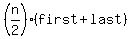 
But in this form of the formula it is not at all apparent why you add the first and last terms and then multiply that by HALF the number of terms.
But if we write that formula in a very slightly different form, then the whole formula makes sense.
--> 
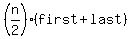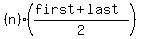
In that form, the formula clearly says that the sum of the terms is the number of terms, times the average of the first and last terms. And since in an arithmetic sequence the average of all the terms is equal to the average of the first and last terms, the formula now states the obvious: the sum is equal to the number of terms times the average of all the terms.
So in my opinion, by far the best formula for finding the sum of the terms of an arithmetic sequence is
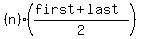
So let's find the answer to the problem without using the actual formula, but rather by understanding that the sum is the number of terms times the average of the terms.
The first row has 16 seats; each row has 2 more seats than the previous row; and there are 46 rows.
The number of seats in the last row is 16+45(2)=16+90=106
The average of the number of seats in all the rows is equal to the average of the numbers of seats in the 1st and 46th rows: (16+106)/2 = 122/1 = 61.
The total number of seats is the number of rows times the average number of seats in each row: 46*61 = 2806
ANSWER: 2806 seats
Answer by ikleyn(52777)  (Show Source):
|
|
|
