Question 1201846: A circular piece of sheet metal has a diameter of 20 in. The edges are to be cut off to form a rectangle of area 150 in2 (see the figure). What are the dimensions of the rectangle? (Round your answers to two decimal places.)
Found 3 solutions by math_tutor2020, greenestamps, ikleyn:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 8.23 inches by 18.23 inches
Each value is approximate.
Explanation:
Here's what the diagram probably looks like

x = horizontal width of the rectangle
y = vertical height of the rectangle
These are positive real numbers
x > 0 and y > 0
area of the rectangle = x*y = 150
Solve for y to get
y = 150/x
Let's focus on triangle ADC.
This is a right triangle.
To see a proof why angle ADC = 90 degrees, search out "Thale's Theorem".
Because ADC is a right triangle, we can use the pythagorean theorem to say:




Let's solve for x.




As a detour, let 
So

and


Use the quadratic formula to solve for w.
Plugging in a = 1, b = -400, c = 22500







 or or 
 (approximate) or (approximate) or  (approximate) (approximate)
If w = 332.287566, then,


 or or 
 or or 
We'll ignore the negative x value because a negative width makes no sense.
Now use that x value to find y



The rectangle has dimensions of:
x = 18.228757
y = 8.228756
If w = 67.712434, then,





Then plugging that into y = 150/x will lead to y = 18.228757
We arrive at the same dimensions as before, but now the x and y values swapped places.
Turns out the order doesn't matter when listing the length and width of a rectangle.
Therefore, the only possible dimensions of the rectangle are roughly 8.23 inches by 18.23 inches when rounding those previous figures to two decimal places.
As a check
x*y = 18.228757 * 8.228756 = 149.999994
which is really close to 150
There's likely some rounding error from a previous step.
And also, we can use the pythagorean theorem to confirm the answer as well
a^2+b^2 = c^2
x^2 + y^2 = 20^2
(18.228757)^2 + (8.228756)^2 = 20^2
400.000007072584 = 400
which isn't too far off either
Answer by greenestamps(13203)   (Show Source): (Show Source):
Answer by ikleyn(52847)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A circular piece of sheet metal has a diameter of 20 in.
The edges are to be cut off to form a rectangle of area 150 in2 (see the figure).
What are the dimensions of the rectangle? (Round your answers to two decimal places.)
~~~~~~~~~~~~~~~~~~
There is more simple solution to this problem (and, therefore, more preferable).
Let x is the longer side of the rectangle and y is its shorter side.
From the description, you have these two equations
xy = 150 (1) (the area)
x^2 + y^ = 20^2 (2) (the diagonal of the rectangle,
which is the diameter of the circle)
Multiply equation (1) by 2 (both sides) and add to equation (2). You will get
x^2 + 2xy + z^2 = 700 (3)
Multiply equation (1) by 2 (both sides) and subtract from equation (2). You will get
x^2 - 2xy + z^2 = 100 (4)
Equations (3) and (4) are equivalent to this system of equations
(x+y)^2 = 700
(x-y)^2 = 100
Taking square roots from both sides of these equations, you arrive to simple system of linear equations
x + y = 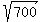 ,
x - y = 10.
or
x + y = ,
x - y = 10.
or
x + y = 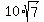 , (5)
x - y = 10. (6)
Add these equations to eliminate y. You will get
2x = , (5)
x - y = 10. (6)
Add these equations to eliminate y. You will get
2x = 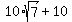 , which implies x = , which implies x = 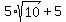 .
Subtract equation (6) from equation (5) to eliminate x. You will get
2y = .
Subtract equation (6) from equation (5) to eliminate x. You will get
2y = 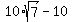 , which implies y = , which implies y = 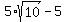 .
ANSWER. x = .
ANSWER. x = 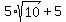 , y = , y = 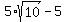 . .
Solved.
|
|
|