SOLUTION: The tangent at the point P(a,b) on the curve y=(ab)/x meets the x axis and y axis at Q and R respectively. show that PQ=RP.

Algebra ->  Systems-of-equations -> SOLUTION: The tangent at the point P(a,b) on the curve y=(ab)/x meets the x axis and y axis at Q and R respectively. show that PQ=RP.      Log On


   

Question 1191761: The tangent at the point P(a,b) on the curve y=(ab)/x meets the x axis and y axis at Q and R respectively. show that PQ=RP.
Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


Here is a diagram with (arbitrarily) (a,b)=(3,8).



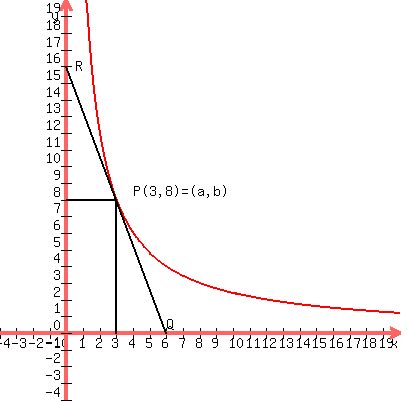
The equation of the curve is

y=ab%2Fx

The derivative of the function is

dy%2Fdx=-ab%2Fx%5E2

The slope of the curve at x=a is the derivative evaluated at x=a:

-ab%2Fa%5E2=-b%2Fa

At this point, to finish the problem, we could do some formal algebra with the point-slope equation of the tangent line to find the x- and y-intercepts and use the distance formula to show that PR=QR.

However, with only a little thought about what we have here, we can see that with a point (3,8) and a tangent at that point with slope (-8/3), moving 3 to the left and 8 up gives us the y-intercept of the tangent line, and moving 3 to the right and down 8 gives us the x-intercept of the tangent line. So the x- and y-intercepts are both the same distance from the point P in both the x- and y-directions, which means the lengths of PQ and PR are equal.