SOLUTION: Min y Kısıtlar x^2 + y^2 ≤ 4 x^2 ≥ 1 yukarıdaki doğrusal olmayan kısıtlı model için olurlu bölgeyi x ve y eksenlerini kullanarak çiziniz ve çizdiğiniz grafiğ

Algebra ->  Systems-of-equations -> SOLUTION: Min y Kısıtlar x^2 + y^2 ≤ 4 x^2 ≥ 1 yukarıdaki doğrusal olmayan kısıtlı model için olurlu bölgeyi x ve y eksenlerini kullanarak çiziniz ve çizdiğiniz grafiğ      Log On


   

Question 1182172: Min y
Kısıtlar x^2 + y^2 ≤ 4
x^2 ≥ 1
yukarıdaki doğrusal olmayan kısıtlı model için olurlu bölgeyi x ve y
eksenlerini kullanarak çiziniz ve çizdiğiniz grafiği kullanarak optimum
değer(ler)i bulunuz.
Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
We translate from Turkish to English, and
we use x for x1 and y for x2.

Minimize y subject to the constraints
x%5E2+%2B+y%5E2+%3C=+4
x%5E2+%3E=+1

For the nonlinear constrained model above, plot the feasible region using
the x and y axes and find the optimum (minimum) value(s) using the graph you
drew.

We draw the boundary graphs, replacing the ≤ and ≥ by =

system%28x%5E2%2By%5E2=4%2Cx%5E2=1%29

Their graphs are the circle with radius 2, and the two vertical lines at 
x = 1 and x = -1. 



We find the points of intersection of the graphs:

system%28x%5E2%2By%5E2=4%2Cx%5E2=1%29

1%2By%5E2=4
y%5E2=3
y=%22%22+%2B-+sqrt%283%29

x%5E2=1
x=%22%22+%2B-+1

The four points of intersection are:

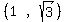
%28matrix%281%2C3%2C1%2C%22%2C%22%2Csqrt%283%29%29%29
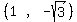
%28matrix%281%2C3%2C1%2C%22%2C%22%2C-sqrt%283%29%29%29
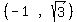
%28matrix%281%2C3%2C-1%2C%22%2C%22%2Csqrt%283%29%29%29
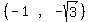%28matrix%281%2C3%2C-1%2C%22%2C%22%2C-sqrt%283%29%29%29

Then the feasible region is:



From the graph, the minimum value of y is -sqrt%283%29

Edwin