SOLUTION: Solve the following simultaneous equations: 3𝑥^2 − 2𝑥𝑦 + 𝑦^2 − 1 = 0 and 𝑥 =(2𝑦+1)/𝑥 .

Algebra ->  Systems-of-equations -> SOLUTION: Solve the following simultaneous equations: 3𝑥^2 − 2𝑥𝑦 + 𝑦^2 − 1 = 0 and 𝑥 =(2𝑦+1)/𝑥 .      Log On


   

Question 1178993: Solve the following simultaneous equations: 3𝑥^2 − 2𝑥𝑦 + 𝑦^2 − 1 = 0 and
𝑥 =(2𝑦+1)/𝑥
.
Found 2 solutions by mananth, Edwin McCravy:
Answer by mananth(16946) About Me  (Show Source):
You can put this solution on YOUR website!
3𝑥^2 − 2𝑥𝑦 + 𝑦^2 − 1 = 0 and
𝑥 =(2𝑦+1)/𝑥
x^2 = (2y+1)
3𝑥^2 − 2𝑥𝑦 + 𝑦^2 − 1 = 0
3(2y+1)^2 -2y(2y+1) -1=0
3(4y^2+4y+1) -4y^2-2y -1=0
12y^2+12y +3 -4y^2-2y-1=0
8y^2+10y+2=0
8y^2+8y+2y+2=0
8y(y+1) +2(y+1)=0
(8y+2)(y+1)=0
y=-1/4 or y=-1
Plug the values of y in x^2=(2y+1)
and get values of x for each y.






Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
The solution above is incorrect due to a careless error:
3𝑥^2 − 2𝑥𝑦 + 𝑦^2 − 1 = 0 and
𝑥 =(2𝑦+1)/𝑥
x^2 = (2y+1)
3𝑥^2 − 2𝑥𝑦 + 𝑦^2 − 1 = 0
3(2y+1)^2 -2y(2y+1) -1=0 <--This step is wrong because she omitted the
y2 term which vitiated the rest.
system%283x%5E2+-+2xy+%2B+y%5E2+-+1+=+0%2C+x=%282y%2B1%29%2Fx%29

x+=%282y%2B1%29%2Fx
x%5E2=2y%2B1
x%5E2-1=2y
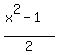%28x%5E2-1%29%2F2=y

Substitute %28x%5E2-1%29%2F2 for y in:

3x%5E2+-+2xy+%2B+y%5E2+-+1+=+0
3x%5E2+-+2x%28%28x%5E2-1%29%2F2%5E%22%22%29+%2B+%28%28x%5E2-1%29%2F2%5E%22%22%29%5E2+-+1+=+0

3x%5E2+-+x%28x%5E2-1%29+%2B+%28x%5E2-1%29%5E2%2F4%5E%22%22+-+1+=+0

Multiply through by 4

12x%5E2+-+4x%28x%5E2-1%29+%2B+%28x%5E2-1%29%5E2+-+4+=+0

12x%5E2+-+4x%5E3%2B4x+%2B+x%5E4-2x%5E2%2B1+-+4+=+0

x%5E4-4x%5E3+%2B+10x%5E2%2B4x-3+=+0

This has no rational zeros, but it has 2 real irrational solutions, which
can be approximated by technology. I used a TI-84 graphing calculator.
Then I substituted the approximation values of x in %28x%5E2-1%29%2F2=y to
find y. The approximations of the solutions are:

(x,y) ≈ (-0.6564052299,-0.2845660870)

(x,y) ≈ (0.40293604482,-0.4188212719) 

Edwin