Question 1174289: Earl solved the following system of equation using substitution.
x + y = 3
2x - 3y = 16
Earl's Solution
2(3-y)-=16
6-y-3y=16
6-4y=16
6-6-4y=16-6
4y=10
-4y=10
-4= -4
y=-2.5
x+(-2.5)=3
x=5.5
Unfortunately, he made a mistake. Locate his error
Found 4 solutions by ewatrrr, Boreal, MathTherapy, greenestamps:
Answer by ewatrrr(24785)   (Show Source):
You can put this solution on YOUR website!
Hi
Earl solved the following system of equation using substitution.
x + y = 3 0r x = (3-y)
2x - 3y = 16 |Earl did make the correct substitution for x
Earl's Solution
2(3-y)-=16 ****|unfortunately Earl forgot the -3y
..........
2(3-y)-3y = 16
6 - 2y - 3y = 16
-5y = 10
y = -2 and x = 5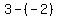 
Ordered pair P(5, -2) the solution for this system of Equations
Checking our work:
2x - 3y = 16
11 + 5 = 16
Wish You the Best in your Studies.
Answer by Boreal(15235)  (Show Source):
Answer by MathTherapy(10551)  (Show Source):
You can put this solution on YOUR website! Earl solved the following system of equation using substitution.
x + y = 3
2x - 3y = 16
Earl's Solution
2(3-y)-=16
6-y-3y=16
6-4y=16
6-6-4y=16-6
4y=10
-4y=10
-4= -4
y=-2.5
x+(-2.5)=3
x=5.5
Unfortunately, he made a mistake. Locate his error
Those 2 are both WRONG!!
The error is NOT with the "- 3y".
The "-" is there on Line 1, but the "3y" is missing. However, the "- 3y" was included on Line 2.
So, it was left out of one of the lines but wasn't forgotten, and was certainly included in the solution!
2(3-y)-=16 <==== Line 1
6-y-3y=16 <===== Line 2
6-4y=16 <======= Line 3
As seen above, the error was made in Line 2 as he DISTRIBUTED the 2 to the (3 - y), but got 6 - y instead of 6 - 2y. That's where the TRUE error lies!
That's all thatw's asked - to find the ERROR! Nothing else!!
Answer by greenestamps(13198)  (Show Source):
You can put this solution on YOUR website!
Ignore the response from tutor @MathTherapy. He likes putting other tutors down by saying their responses are wrong.
Friendly ways of correcting other tutors' responses would be writing a correct solution, or writing a response point out the other tutor's errors to the tutor so they can correct them.
But this tutor shows arrogance and disrespect in his attacks on other tutors.
In this case, the responses from the other two tutors showed the correct mistake in Earl's solution; his did not.
|
|
|
