Question 1152325: It is not a system, I can not find anything, anywhere that is just solving one nonlinear equation.
x/(x+1)>3x
1. Work the problem
2. Set to zero and factor.
3. Find zeros.
4. Find intervals.
5. Test intervals.
6. Write answer in interval notation and graph.
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Below is the plot of two functions, y = 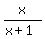 (in red) and y = 3x (in green). (in red) and y = 3x (in green).
The problem is to find where the red line is above the green line.
 Plot y =
Plot y = 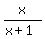 (red) and y = 3x (green). (red) and y = 3x (green).
From the plot, it is clear that the solution is the union of TWO intervals:
one interval is semi-infinite ( , , ) and the other interval is somewhere between -1 and 0. ) and the other interval is somewhere between -1 and 0.
The solution by @MathLover1 gives only the second interval and entirely misses the first semi-infinite interval.
So, her solution is INCORRECT. Therefore, I came to bring the correct solution.
After completing my solution, I will point the error in the MathLover1' solution.
So, we start from the given inequality
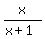 > 3x. (1)
Move 3x to the left side > 3x. (1)
Move 3x to the left side
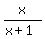 - 3x > 0
Write with the common denominator - 3x > 0
Write with the common denominator
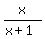 - - 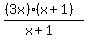 > 0
Make equivalent transformations > 0
Make equivalent transformations
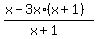 > 0 > 0
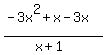 > 0 > 0
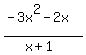 > 0 > 0
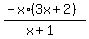 > 0
Multiply both sides by (-1) and change the inequality sign > 0
Multiply both sides by (-1) and change the inequality sign
 < 0.
Divide by 3 both sides < 0.
Divide by 3 both sides
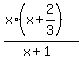 < 0. (2)
So, our original inequality is equivalent to the inequality (2).
Now I will solve the inequality (2).
The factors in inequality (2) have three critical points, where linear terms become equal to zero and change the sign.
These points are -1, < 0. (2)
So, our original inequality is equivalent to the inequality (2).
Now I will solve the inequality (2).
The factors in inequality (2) have three critical points, where linear terms become equal to zero and change the sign.
These points are -1,  and 0.
The critical points divide the entire number line in four intervals
1) ( and 0.
The critical points divide the entire number line in four intervals
1) ( , , ), 2) ( ), 2) ( , , ), 3) ( ), 3) ( , , ) and 4) [ ) and 4) [ , , ).
In the interval #1, all three linear factors are negative, so the entire rational function is negative.
Thus the entire interval ( ).
In the interval #1, all three linear factors are negative, so the entire rational function is negative.
Thus the entire interval ( , , ) IS the solution to inequality (2) and, hence, for the original inequality, too.
In the interval #2, the linear factor (x+1) is positive, while two other factors are negative,
so the entire rational function is positive.
Thus the interval ( ) IS the solution to inequality (2) and, hence, for the original inequality, too.
In the interval #2, the linear factor (x+1) is positive, while two other factors are negative,
so the entire rational function is positive.
Thus the interval ( , , ) is NOT the solution to inequality (2) and, hence, is NOT the solution for the original inequality.
In the interval #3, the linear factors (x+1) and ) is NOT the solution to inequality (2) and, hence, is NOT the solution for the original inequality.
In the interval #3, the linear factors (x+1) and 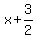 are both positive, while third factor x is negative,
so the entire rational function is negative.
Thus the interval ( are both positive, while third factor x is negative,
so the entire rational function is negative.
Thus the interval ( , , ) IS the solution to inequality (2) and, hence, IS the solution for the original inequality.
In the interval #4, all three linear factors are positive, so the entire rational function in (2) is positive.
Thus the interval [ ) IS the solution to inequality (2) and, hence, IS the solution for the original inequality.
In the interval #4, all three linear factors are positive, so the entire rational function in (2) is positive.
Thus the interval [ , , ) is NOT the solution to inequality (2) and, hence, is not the solution for the original inequality.
ANSWER. The solution set for the given inequality is the union of two intervals ( ) is NOT the solution to inequality (2) and, hence, is not the solution for the original inequality.
ANSWER. The solution set for the given inequality is the union of two intervals ( , , ) U ( ) U ( , , ).
Please notice and pay special attention that all endpoints are treated correctly in my solution and in my answer. ).
Please notice and pay special attention that all endpoints are treated correctly in my solution and in my answer.
The problem is solved, and solved correctly.
The way on how I solved it, is a STANDARD (but not a unique) way solving such inequalities for rational functions.
-----------
Now, I promised to show where is the error in the solution by @MathLover1.
It is in the 4-th line of her post, where she multiplies both sides of the inequality by the factor (x+1)
without analyzing the sign of this factor.
Doing in this way, she gets NON-EQUIVALENT inequality and comes to the wrong resulting answer.
It is very common error in solving such inequalities for rational functions - so, be aware (!)
At this point, I completed my post.
From it, learn on how to solve similar problems correctly.
-----------------
If you want to see many other similar solved problems, look into the lessons
- Solving inequalities for rational functions with numerator and denominator factored into a product of linear binomials
- Solving inequalities for rational functions with non-zero right side
in this site.
Consider these lessons as your handbook, textbook, tutorials and (free of charge) home teacher.
|
|
|