SOLUTION: A cashier box has 3 types of coins (nickels, dimes and quarters). There are a total of 88 coins with a total value of $14.55. If the number of quarters is double that of number of

Algebra ->  Systems-of-equations -> SOLUTION: A cashier box has 3 types of coins (nickels, dimes and quarters). There are a total of 88 coins with a total value of $14.55. If the number of quarters is double that of number of      Log On


   

Question 1136557: A cashier box has 3 types of coins (nickels, dimes and quarters). There are a total of 88 coins with
a total value of $14.55. If the number of quarters is double that of number of nickels, how many
of each coins are there?
Found 2 solutions by josmiceli, ikleyn:
Answer by josmiceli(19441) About Me  (Show Source):
You can put this solution on YOUR website!
(1) +q+=+2n+
(2) +n+%2B+d+%2B+q+=+88+
(3) +5n+%2B+10d+%2B+25q+=+1455+ ( in cents )
------------------------------------------------
There are 3 equations and 3 unknowns
so it's solvable

Answer by ikleyn(52775) About Me  (Show Source):
You can put this solution on YOUR website!
.
Let N be the number of nickels.


Then the number of quarters is 2N, according to the condition,
and the number of dimes is the rest (88 - N - 2N) = 88-3N.


The "money" equation then is


    5N + 10*(88-3N) + 25*(2N) = 1455 cents.


Simplify and solve for N


    5N + 880 - 30N + 50N = 1455

    25N = 1455 - 880

    25N = 575  =============>  N = 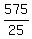575%2F25 = 23.


ANSWER.  23 nickels,  2*23 = 46 quarters and  88-23-46 = 19 dimes.


CHECK.   23*5 + 46*25 + 19*10 = 1455 cents.    ! Correct !

Solved.

-------------------

The lesson to learn from my post is THIS : 

    This problem is to be solved by reduction to one single equation in one unknown.