Question 1113181: The function 4.3x+y=198 models the number of land-line phone customers, in millions, x years after 2000. The function y=19.8x+98 models the number of cell phone customers, in millions, x years after 2000.
a. Use these models to determine the year, rounded to nearest year, when the number of cell phone and landline customers is the same.
b. according to the models, how many customers were there for each type of phone customer for the year determined in part a. (rounded to the nearest ten million)?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! put both functions into the same form.
i chose slope intercept form.
the function 4.3x + y = 198 becomes y = -4.3x + 198
the function y = 19.8x + 98 is already in slope intercept form.
you have 2 equations that need to be solved simultaneously.
they are:
y = -4.3x + 198
y = 19.8x + 98
to eliminate the y variable, subtract the second equation from the first to get:
0 = -24.1x + 100
add 24.1x to both sides of the equation to get:
24.1x = 100
solve for x to get:
x = 100 / 24.1 = 4.149377593
this means the number of landline customers will be equal to the number of cell phone customer sometime in the 4th year after 2000.
that would be 2004.
you can graph this equation.
it would look like this:
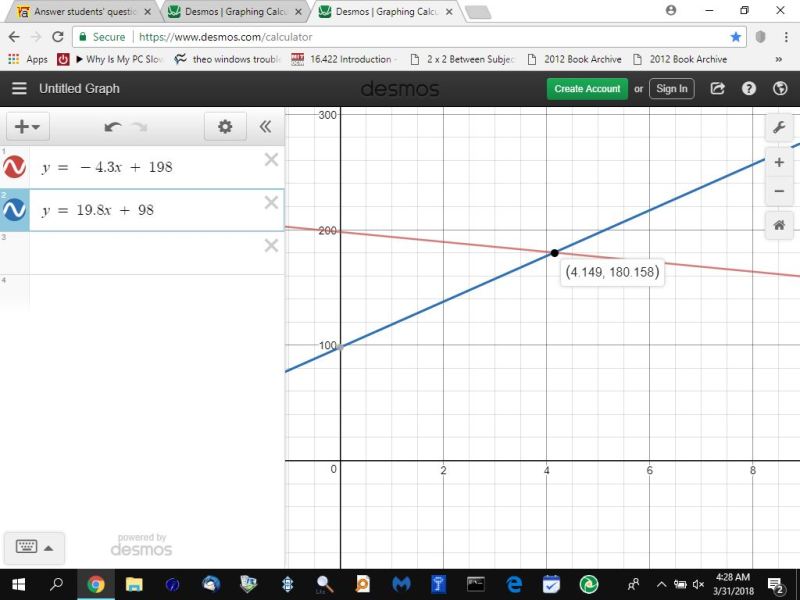
if you want x to represent the actual year, then you need to shift the graph over to the right by 2000.
that graph would look like this.
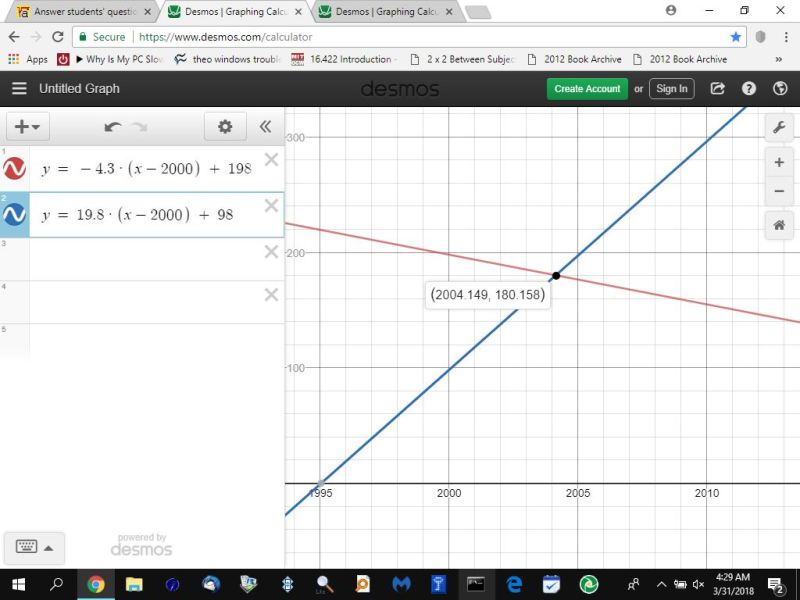
your questions and answers to them are shown below:
a. Use these models to determine the year, rounded to nearest year, when the number of cell phone and landline customers is the same.
that would be sometime in 2004.
b. according to the models, how many customers were there for each type of phone customer for the year determined in part a. (rounded to the nearest ten million)?
when they were equal, the number of customers was 180.1576763 million.
round this to the nearest 10 million and it becomes 180 million.
|
|
|