SOLUTION: The perimeter of a right triangle is 144 cm. The base is 12 cm. less than the adjacent. Find the area.

Algebra ->  Systems-of-equations -> SOLUTION: The perimeter of a right triangle is 144 cm. The base is 12 cm. less than the adjacent. Find the area.      Log On


   

Question 1108272: The perimeter of a right triangle is 144 cm. The base is 12 cm. less than the adjacent. Find the area.
Found 2 solutions by KMST, ikleyn:
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
The easiest way to calculate the area of a right triangle is
area=%281%2F2%29%2Aleg%5B1%5D%2Aleg%5B2%5D ,
because the legs are perpendicular to each other,
so one leg can be considered the base, and the other is the height.
The difficult part is calculating the length of those legs.
The sides of the triangle measure
leg%5B1%5D=36cm , leg%5B2%5D=48cm and hypotenuse=60cm .
In this case,
area=%281%2F2%29%2A%2836cm%29%2A%2848cm%29=highlight%28864cm%5E2%29
How did I know the leg length?

THE GET RESULTS WITHOUT MUCH WORK WAY:
Looking at a list of Pythagorean triples,
or looking at multiples of the popular 3-4-5 triple,
we figure that 36-48-60 (the 3-4-5 triple times 12)
add up to 144, and there are differences of 12 between the numbers.
The sum of the numbers, and differences between numbers in 3-4-5
are 12 and 1 respectively, so after multiplying everything times 12,
the sum and differences are
23%2A12=144 and 1%2A12=12

THE EXPECTED WAY:
If there is a figure, it may suggest that
the "base" is one leg of the right triangle.
If we think the base is the shorter leg,
"the adjacent" can be taken to mean the other leg or the hypotenuse.
If we think the base is the longer leg, then "the adjacent" must be the hypotenuse.
Either way, what follows is not fun.
If we think "the adjacent" is the hypotenuse,
the lengths of the sides of the triangle, in cm, are:
x= hypotenuse,
x-12= the "base" leg,
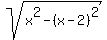sqrt%28x%5E2-%28x-2%29%5E2%29=the other leg, and
the perimeter (in cm) is
x%2Bx-12%2Bsqrt%28x%5E2-%28x-12%29%5E2%29=144
2x-12%2Bsqrt%28x%5E2-%28x%5E2-24x%2B144%29%29=144
2x-12%2Bsqrt%28x%5E2-x%5E2%2B24x-144%29=144
2x-12%2Bsqrt%2824x-144%29=144
sqrt%2824x-144%29=144%2B12-2x
sqrt%2824x-144%29=156-2x
If we get smart, our next step is
2sqrt%286x-36%29=156-2x ,
an then we simplify, dividing both sides by 2,to get
sqrt%286x-36%29=78-x .
Squaring both sides of the equal sign, we get
6x-36=6084-156%2Bx%5E2
x%5E2-156x-6x%2B6084%2B36=0
x%5E2-162x%2B6120=0
AT that point, we may be able to factor it as
%28x-60%29%28x-102%29=0 .
The solutions to that equation are x=60 and x=102 .
We discard x=102 ,
because it is not a solution of sqrt%286x-36%29=78-x .
It is just an extraneous solution we introduced when we squared both sides.
The conclusion is that the hypotenuse measures 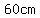60cm ,
the base measures 60cm-12cm=48cm ,
and the length of the other leg, in cm, is


If there is another way that is simple, let me know.

Answer by ikleyn(52776) About Me  (Show Source):
You can put this solution on YOUR website!
.
The perimeter of a right triangle is 144 cm. The base is 12 cm. less than the adjacent. Find the area.
~~~~~~~~~~~~~~~~~~~~~~

The person who posted it, simply does not know the terminology.

Concretely, he does not know that the perpendicular sides of a right-angled triangle are called the legs.

It is the source of difficulties that some tutors have trying to find the sense, hidden behind wrong terminology usage.

The correct formulation of the problem is  THIS: 

    The perimeter of a right triangle is 144 cm. One leg is 12 cm shorter than another. Find the area.

In this formulation  (in this interpretation)  the problem was solved under this link
https://www.algebra.com/algebra/homework/Systems-of-equations/Systems-of-equations.faq.question.1108259.html

https://www.algebra.com/algebra/homework/Systems-of-equations/Systems-of-equations.faq.question.1108259.html


But the original formulation in the post  #1108259  was wrong again, and I pointed to it to the author of the post.