.
Let x and y be the two numbers under the question.
Then their reciprocals are  and
and  , and the condition says
, and the condition says
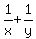 = 5, (1)
= 5, (1)
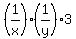 = 18. (2)
The last equation is equivalent to
= 18. (2)
The last equation is equivalent to
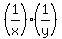 = 6. (3)
So, you need to solve the system (1),(3).
To make it easier, introduce new variables a =
= 6. (3)
So, you need to solve the system (1),(3).
To make it easier, introduce new variables a =  , b =
, b =  .
Then the system (1),(3) takes the form
a + b = 5, (4)
ab = 6. (5)
From (4), a = 5-b. Substitute it into (4). You will get
(5-b)*b = 6,
5b - b^2 = 6,
b^2 - 5b + 6 = 0,
(b-2)*(b-3) = 0.
The roots are
.
Then the system (1),(3) takes the form
a + b = 5, (4)
ab = 6. (5)
From (4), a = 5-b. Substitute it into (4). You will get
(5-b)*b = 6,
5b - b^2 = 6,
b^2 - 5b + 6 = 0,
(b-2)*(b-3) = 0.
The roots are  = 2 and
= 2 and  = 3.
1. If b = 2, then a = 3, and x =
= 3.
1. If b = 2, then a = 3, and x =  , y =
, y =  .
2. If b = 3, then a = 2, and x =
.
2. If b = 3, then a = 2, and x =  , y =
, y =  .
Answer. The two numbers are
.
Answer. The two numbers are  and
and  .
.
Solved.