Question 1078281: Find an ordered triple (x,y,z) of real numbers satisfying the system of equations
sqrt{x} + sqrt{y} + sqrt{z} = 10,
x + y + z = 38,
sqrt{xyz} = 30,
or, if there is no such triple, enter the word "none" as your answer.
Found 2 solutions by Alan3354, ikleyn:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find an ordered triple (x,y,z) of real numbers satisfying the system of equations
sqrt{x} + sqrt{y} + sqrt{z} = 10,
x + y + z = 38,
sqrt{xyz} = 30,
or, if there is no such triple, enter the word "none" as your answer.
================
(4,9,25)
-----------
What did you learn from that?
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
.
Find an ordered triple (x,y,z) of real numbers satisfying the system of equations
sqrt{x} + sqrt{y} + sqrt{z} = 10,
x + y + z = 38,
sqrt{xyz} = 30,
or, if there is no such triple, enter the word "none" as your answer.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let me introduce new variables u =  , v = , v = 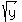 , and w = , and w =  .
Then I can rewrite the given equations in this form:
u + v + w = 10, (1) .
Then I can rewrite the given equations in this form:
u + v + w = 10, (1)
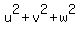 = 38, (2)
u*v*w = 30. (3)
From (1) and (2) = 38, (2)
u*v*w = 30. (3)
From (1) and (2)
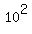 = 100 = = 100 = 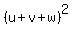 = = 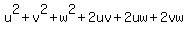 = 38 + 2(uv + uw + vw),
hence, 2(uv + uw + vw) = 100 - 38 = 62, and uv + uw + vw = 31.
Now I can rewrite the system (1),(2),(3) in the form
u + v + w = 10, (1')
uv + uw + vw = 31, (2')
u*v*w = 30. (3')
It means ( !! The Vieta's formulas !! ) that u, v ans w are the roots of this cubical equation
X^3 - 10X^2 + 31X - 30 = 0. (4)
Now you can apply the "Rational roots Theorem" which says that the rational (in particular, integer) roots of the equation (4)
are among the divisors of the constant term 30.
Or even better, you can make a plot of the left side polynomial which (the plot) will say you a lot about the roots: = 38 + 2(uv + uw + vw),
hence, 2(uv + uw + vw) = 100 - 38 = 62, and uv + uw + vw = 31.
Now I can rewrite the system (1),(2),(3) in the form
u + v + w = 10, (1')
uv + uw + vw = 31, (2')
u*v*w = 30. (3')
It means ( !! The Vieta's formulas !! ) that u, v ans w are the roots of this cubical equation
X^3 - 10X^2 + 31X - 30 = 0. (4)
Now you can apply the "Rational roots Theorem" which says that the rational (in particular, integer) roots of the equation (4)
are among the divisors of the constant term 30.
Or even better, you can make a plot of the left side polynomial which (the plot) will say you a lot about the roots:
 Plot y =
Plot y = 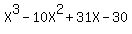 From the plot, it is clearly seen that the roots u, v and w are 2, 3 and 5 (from smaller to greater).
You can check it manually.
Hence, the solution to the original system is (x,y,z) = (4,9,25) and all possible permutations.
From the plot, it is clearly seen that the roots u, v and w are 2, 3 and 5 (from smaller to greater).
You can check it manually.
Hence, the solution to the original system is (x,y,z) = (4,9,25) and all possible permutations.
Isn't this solution is beautiful ?
The tutor "Alan" asked in his post, what we can learn from this problem ?
The answer is: THIS BEAUTIFUL SOLUTION and THIS BEAUTIFUL METHOD.
I just had a chance to solve one similar problem before. See the lesson
- Solving systems of non-linear algebraic equations with symmetric functions of unknowns
in this site.
|
|
|