Question 1062395: I am trying to figure how to find part of answer to this non-linear system:
(X+1)^2 - (y-1)^2 = 20
X^2 - (y+2)^2 = 24
I used elimination to end up with the answers of y = 1/2 and x = -11/2.
This has been confirmed via graphing. Problem is there is another common point of 5,-3, but I cannot figure out how to come do it algebraically. Any help would be appreciated. Thank you!
Answer by ikleyn(52933)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
(x+1)^2 - (y-1)^2 = 20
x^2 - (y+2)^2 = 24
~~~~~~~~~~~~~~~~~~~~~~~~~~
(x+1)^2 - (y-1)^2 = 20, (1)
X^2 - (y+2)^2 = 24. (2)
Open parentheses:
x^2 + 2x + 1 - y^2 + 2y - 1 = 20, (3)
x^2 - y^2 - 4y - 4 = 24. (4)
Distract (4) from (3) (both sides). You will get
2x + 1 + 6y + 3 = -4, or
2x + 6y = -8, or
x + 3y = -4. (5)
Express x = -3y - 4 from (5) and substitute it into (2), replacing x. You will get
(-3y - 4)^2 - (y+2)^2 = 24, or
9y^2 + 24y + 16 - y^2 - 4y - 4 = 24, or
8y^2 + 20y - 12 = 0, or
2y^2 + 5y - 3 = 0.
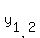 = =  = = 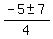 .
The roots are .
The roots are  = =  , ,  = -3.
For each root = -3.
For each root 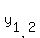 find the corresponding value of x.
Can you complete it on your own? find the corresponding value of x.
Can you complete it on your own?
If you want to see more similar solved problems, look into the lesson
- Solving systems of algebraic equations of degree 2
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic "Systems of equations that are not linear".
|
|
|