Question 1062359: The system of equations I need to solve is:
7x - 8y = 24
xy^2 = 1
In the second, it's not (xy)^2, but just the y is squared. I get to substitution and replace y in the second equation with y = (7/8)x + 3 and end up with (23/32)x^3 + (21/4)x^2 + 9x - 1 = 0. My professor warned that this problem is pure evil and said at this point I would need to use rational root theorem and that there IS a rational root. Issue is I don't know how to find a rational root from a fraction as a leading coefficient (23/32).... Unless I screwed up before that and that's not what I'm looking at.
Any help to get me beyond this point will be greatly appreciated.
Found 2 solutions by Alan3354, MathTherapy:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! The system of equations I need to solve is:
7x - 8y = 24
xy^2 = 1
In the second, it's not (xy)^2, but just the y is squared. I get to substitution and replace y in the second equation with y = (7/8)x + 3 and end up with (23/32)x^3 + (21/4)x^2 + 9x - 1 = 0.
--------------
7x - 8y = 24 --> y = (7/8)x -3 *** not +3
x*(7x/8 - 3)^2 - 1 = 0
x*(49x^2/64 - 21x/32 + 9) -1 = 0
49x^3/64 - 21x^2/32 + 9x - 1 = 0
Multiply by 64
49x^3 - 42x^2 + 576x - 64 = 0
===============
The only real root I see is ~ 0.111905 (by graphing)
Answer by MathTherapy(10551)   (Show Source): (Show Source):
You can put this solution on YOUR website! The system of equations I need to solve is:
7x - 8y = 24
xy^2 = 1
In the second, it's not (xy)^2, but just the y is squared. I get to substitution and replace y in the second equation with y = (7/8)x + 3 and end up with (23/32)x^3 + (21/4)x^2 + 9x - 1 = 0. My professor warned that this problem is pure evil and said at this point I would need to use rational root theorem and that there IS a rational root. Issue is I don't know how to find a rational root from a fraction as a leading coefficient (23/32).... Unless I screwed up before that and that's not what I'm looking at.
Any help to get me beyond this point will be greatly appreciated.
It's not that bad as your professor professed.
 ------- eq (ii) ==========> You got up to this point ------- eq (ii) ==========> You got up to this point
You have: 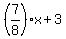 , but it should be: , but it should be: 
 ----- Substituting ----- Substituting 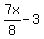 for y in eq (ii) for y in eq (ii)
 ----- FOILing ----- FOILing 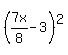

 ---- Multiplying TRINOMIAL in parentheses by LCD, 64 ---- Multiplying TRINOMIAL in parentheses by LCD, 64
 ------ Cross-multiplying ------ Cross-multiplying
 ------- Distributing left-side ------- Distributing left-side
 ---- Subtracting 64 from each side ---- Subtracting 64 from each side
Now is the time you use the rational root theorem with factors of 49 or 64. You will find that 4 is a root, so: x = 4, and x - 4 is a factor.
Using the factor x - 4, and SYNTHETIC DIVISION or LONG DIVISION of POLYNOMIALS, you will find that the QUOTIENT when 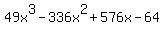 is divided by x - 4 is: is divided by x - 4 is: 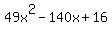 . .
Therefore, the factors of 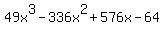 are are 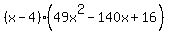 . .
You just need to use the quadratic equation formula or COMPLETING THE SQUARE to get the final 2 factors of 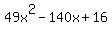 , which happen to be REAL also (2.73787877 and 0.1193). , which happen to be REAL also (2.73787877 and 0.1193).
You have 3 values for x, so substitute each one into the SIMPLER original equation [eq (i) or (ii)] to find each CORRESPONDING y-value.
That's it!! The trick here is to do things in STEPS, or LITTLE by LITTLE. That way, you won't be confused and make mistakes.
|
|
|