.
Please help me solve this by using the substitution method. Thank you!


~~~~~~~~~~~~~~~~~~~~~~
 = 90, (1)
y =
= 90, (1)
y =  . (2)
Square equation (2) (both sides). You will get
. (2)
Square equation (2) (both sides). You will get
 = x.
Using this, replace
= x.
Using this, replace  by "x" in the equation (2). You will get
by "x" in the equation (2). You will get
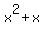 = 90, (1') or
= 90, (1') or
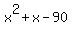 = 0.
Solve by using the quadratic formula. You will get
= 0.
Solve by using the quadratic formula. You will get
 =
= 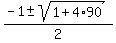 =
= 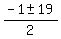 .
Thus
.
Thus  = 9,
= 9,  = -10.
Since "x" under the square root must be non-negative, only the root x= 9 survives.
Then y =
= -10.
Since "x" under the square root must be non-negative, only the root x= 9 survives.
Then y =  = +/- 3.
Answer. There are 2 solutions: (x,y) = (9,3) and (x,y) = (9,-3).
= +/- 3.
Answer. There are 2 solutions: (x,y) = (9,3) and (x,y) = (9,-3).