SOLUTION: Vertices of a regular octagon are connected as shown. What fraction of the octagon is shaded? Link to graph: https://ibb.co/gFTD6Rg

Let "a" be the side length of this regular octagon.


Then the area of the whole octagon is (3a)^2 - 2a^2 = 9a^2 - 2a^2 = 7a^2.


It is because the area of the square accommodating the octagon is (3a)^2,
from which we should subtract/(cut) four halves of squares with side length "a".


OK.  Now, in the picture, we have the shadowed triangle and another, greater triangle,
that accommodates the shadowed triangle.


This greater triangle area is, obviously, 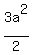 , since this greater triangle is half 
of the rectangle with sides "a" and 3a.


Now our goal is to estimate the area of the shadowed triangle.


These two triangles, the shadowed and the greater one, are right-angled triangles with the common
acute angle. So, these two triangles are similar.


To estimate the area of the shadowed triangle, it is enough to find the coefficient of similarity 
of the triangles.


Compare the longest legs of these two triangles.


For the greater  triangle, the length of its longest leg is 3a.

For the shadowed triangle, the length of its longest leg is the radius of the circumscribed circle 
about the regular octagon.


The formula expressing the radius of the circumscribed circle via the side of the regular octagon is

    r = .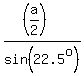


So, the similarity coefficient for the two triangles is (as the ratio of the smaller to the larger)

    k =  =  = .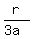


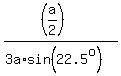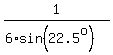Well known fact is that sin(22.5°) = .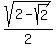


Therefore, the similarity coefficient for the two triangles is  

    k =  = .


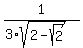Thus the area of the shadowed triangle is

    area =  =  = .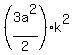


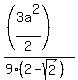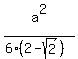To calculate the fraction of the area, we should relate it to 7a^2, the area of the regular octagon.


Thus the  ANSWER  is:  fraction = 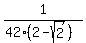 = 0.0406454  (approximately).