SOLUTION: five cones A, B, C, D and E are mathematically similar. their heights are in the ratio 2:3:4:5:6 Cone B has height 3.6cm and surface area 45cm^2. a) work out height of cone C.

Algebra ->  Surface-area -> SOLUTION: five cones A, B, C, D and E are mathematically similar. their heights are in the ratio 2:3:4:5:6 Cone B has height 3.6cm and surface area 45cm^2. a) work out height of cone C.      Log On


   

Question 975313: five cones A, B, C, D and E are mathematically similar.
their heights are in the ratio 2:3:4:5:6
Cone B has height 3.6cm and surface area 45cm^2.
a) work out height of cone C.
b) work out the surface area of cone D.
c) Cone A is used to fill cone E with sand. how many full cones of sand from cone A are needed to fill cone E?

Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
In the following I will use h, S and V respectively for height,
surface area and volume, respectively, with subscripts A,B,C,D,E
referring to the particular cones they are of.

five cones A, B, C, D and E are mathematically similar.
their heights are in the ratio 2:3:4:5:6

2:3:4:5:6 = 2k:3k:4k:5k:6k for any non-zero constant k

a) work out height of cone C.
hA:hB:hC:hD:hE = 2k:3k:4k:5k:6k
for any positive k

Let's find the particular positive k such that 

hA=2k, hB=3k, hC=4k, hD=5k, hE=6k,

Cone B has height 3.6cm
hB = 3k
 
3.6 = 3k
1.2 = k

Then with that constant k = 1.2, we can find any of the heights.
In particular,

hC = 4k = 4(1.2) = 4.8cm

b) work out the surface area of cone D.
Proportions of corresponding areas are the squares of the proportions of
corresponding linear measures.

SA:SB:SC:SD:SE = 22:32:42:52:62 = 4:9:16:25:36 = 4k:9k:16k:25k:36k 
for any positive k

Let's find the positive k such that 

SA=4k, SB=9k, SC=16k, SD=25k, SE=36k,

Cone B has...surface area 45cm^2. 
SB = 9k
 
45 = 9k
5 = k

Then with that constant k=5, we can find any of the surface areas.
In particular,

SD = 25k = 25(5) = 125cm2

c) Cone A is used to fill cone E with sand. how many full cones of sand
from cone A are needed to fill cone E?
Proportions of corresponding volumes are the cubes of the proportions of
corresponding linear measures.

VA:VB:VC:VD:VE = 23:33:43:53:63 = 8:27:64:125:216 = 8k:27k:64k:125k:216k
for any positive k

There exists positive k such that 

VA=8k, VB=27k, VC=64k, VD=125k, VE=216k, 

But we don't need to find that value of k as we did in the other two. We
simply divide VE = 216k by VA=8k, and the k's will cancel.

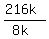%28216k%29%2F%288k%29 = 27 full cones of sand from cone A are needed to fill cone E.

Edwin