Question 969785: Each side of the squares equals to 7units.
How do I calculate the area of an equilateral triangle inside the square with sides 7units?
How do I work out the area of a circle inside a square with sides equal to 7 units?
What would the ratio be of area of triangle:area of circle?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! EQUILATERAL TRIANGLE:
The area of a triangle with sides of lengths  , ,  , and , and  , ,
opposite angles of measures  , ,  , and , and  , ,
can be calculated as  : :

In the case of an equilateral triangle,
all sides have the same length,  , ,
and all angles measure  , ,
so  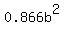 . .
If your equilateral triangle inside a square looks like this  , ,
then  and and  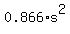 . .
  . .
However, it may not be the expected answer,
but you may be able to fit a slightly larger triangle if you "tilt" it,
like this  . .
CIRCLE:
The larges circle that you would be able to fit inside a square has a diameter as long as the side of the square:
 If the square side length is If the square side length is  , the circle radius is , the circle radius is 
The area of a circle of radius  , ,
so a circle of radius  . .
In particular, for 
the area would be  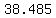 . .
For the triangle and circle described above,
the ratio of their areas would be
 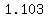 . .
(The side of the square  did not matter, as long as we use the same square size to fit the triangle and the circle). did not matter, as long as we use the same square size to fit the triangle and the circle).
LARGER TRIANGLE:
 In the right triangle corners, according to the Pythagorean theorem, In the right triangle corners, according to the Pythagorean theorem,
 and and  , so , so





 , and since , and since 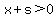 and and 


 , and , and  . .
Now, we knew that for a triangle,  , ,
and that this tilted triangle has  , ,
so  and and   . .
That makes the area of thte tilted triangle
approximately  , ,
and the ratio of areas for the tilted triangle and circle would be
 . .
That ratio is approximately 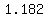 . .
|
|
|