SOLUTION: what dimensions would a rectangular prism have if its surface area was 160 fee square. Based on the answer what would the figure's volume be.

Algebra ->  Surface-area -> SOLUTION: what dimensions would a rectangular prism have if its surface area was 160 fee square. Based on the answer what would the figure's volume be.      Log On


   

Question 968969: what dimensions would a rectangular prism have if its surface area was 160 fee square. Based on the answer what would the figure's volume be.
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
Let X , Y , and Z be the dimensions (in feet) of the rectangular prism.
Let's say X%3C=Y%3C=Z .

The surface area of the base of that {box) is YZ square feet.
The surface area of the top of that {box) is YZ square feet.
The surface area of the sides of that {box) is 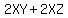2XY%2B2XZ square feet.
The total surface area of the base of that {box) in square feet is
is 2XY%2B2XZ%2B2YZ=2%28XY%2BXZ%2BYZ%29 .
We are told that the total surface area is 160 square feet, so we know that
2%28XY%2BXZ%2BYZ%29=160<--->XY%2BXZ%2BYZ=160%2F2<--->XY%2BXZ%2BYZ=80 .
We can give values to X and Y and solve for Z .
Then we can calculate the volume of that box (in cubic feet) as
Volume=X%2AY%2AZ , by multiplying together X , Y , and Z .

Let's say that system%28X=1%2C%22and%22%2CY=2%29 .
Then, substituting those values, we get
1%2A2%2B1%2AZ%2B2%2AZ=80-->2%2BZ%2B2Z=80-->2%2B3Z=80-->3Z=80-2-->3Z=78-->Z=78%2F3-->Z=26 .
Volume=1%2A2%2A26=52 .

Let's say that system%28X=1%2C%22and%22%2CY=8%29 .
Then, substituting those values, we get
1%2A8%2B1%2AZ%2B8%2AZ=80-->8%2B9Z=80-->9Z=80-8-->9Z=72-->Z=72%2F8-->Z=8 .
Volume=1%2A8%2A8=64 .

Let's say that system%28X=2%2C%22and%22%2CY=2%29 .
Then, substituting those values, we get
2%2A2%2B2%2AZ%2B2%2AZ=80-->4%2B4Z=80-->4Z=80-4-->4Z=76-->Z=76%2F4-->Z=19 .
Volume=2%2A2%2A19=76 .

If we start with system%28X=2%2C%22and%22%2CY=4%29 , we find
system%28Z=12%2C%22and%22%2CVolume=96%29 .

If we start with system%28X=2%2C%22and%22%2CY=5%29 , we find
system%28Z=10%2C%22and%22%2CVolume=100%29 .

If we start with system%28X=4%2C%22and%22%2CY=4%29 , we find
system%28Z=8%2C%22and%22%2CVolume=128%29 .

Other choices yield measurements that are not whole numbers.
For example, if we start with system%28X=5%2C%22and%22%2CY=5%29 , we find
system%28Z=5.5%2C%22and%22%2CVolume=137.5%29 ,
and if we wanted a cube, with X=Y=Z, we would have
X%2AY%2BX%2AZ%2BY%2AZ=80--->X%2AX%2BX%2AX%2BX%2AX=80--->X%5E2%2BX%5E2%2BX%5E2=80--->3X%5E2=80--->X%5E2=80%2F3--->Z=Y=X=sqrt%2880%2F3%29=4sqrt%285%2F3%29=4sqrt%2815%29%2F3=about5.164
and

NOTE:
The way to answer the question depends on the math level of the class where this question was asked.
Was it asked in elementary school? In a college advanced calculus class? somewhere in between.
I do not believe this is a question from a multivariate calculus class, but intuition would tell us that the rectangular prism with greatest volume will be a cube.