Question 965885: A group of parents are planning a children’s playground. In order to save on fencing, they are positioning the playground so that one side is immediately adjacent to the school building. If the playground is to be a rectangle 500 square yards in area, what dimensions should they use if they want to use the least amount of fencing?.
Found 2 solutions by Theo, KMST:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! let l = the length and let w equal the width.
the area is equal to l*w.
since the area has to be 500 square feet, then you get 500 = l * w.
solve for w to get w = 500 / l.
the perimeter will be equal to l + 2w.
normally the perimeter is equal to 2l + 2w, but one of the lengths will be the side of the school, so you only need one l.
since w = 500 / l, the perimeter becomes equal to l + 2 * 500/l
set y = the perimeter and set x equal the length and the formula for perimeter becomes:
y = x + 2*500 / x
this can be simplified to y = x + 1000 / x
you want to minimize the perimeter which means you want to minimize y.
if you graph y = x + 1000 / x, you can see where y will be at a minimum.
the graph looks like this:

since both x and y have to be greater than 0, you are looking at the right side of the y-axis and above the x-axis on the graph.
your problem is to find the minimum point on the graph.
some graphing software will tell you what it is.
other graphing software will not.
in the absence of graphing software that will tell you, or a minimum point formula you can use, you need to use calculus to find it.
the derivative of the equation set to 0 will give you the min/max point of the equation.
the equation is y = x + 1000 / x
the derivative with respect to x is y' = 1 - 1000 / x^2
set this equal to 0 and you get 1 - 1000 / x^2 = 0
add 1000 / x^2 to both sides of this equation to get 1 = 1000 / x^2
solve for x^2 to get x^2 = 1000
solve for x to get x = plus or minus 31.6227766.
since x has to be positive, then x = 31.6227766.
since x represents the length, and the area is equal to the length * width, and the area is equal to 500, you get 500 = 31.6227766 * the width.
solve for the width to get the width = 15.8113883.
the perimeter is equal to the length plus 2 times the width, so the perimeter will be 31.6227766 + 2 * 15.8113883 which makes the perimeter equal to 63.2455532.
placing y = 63.2455532 on the grpah will show you that is the minimum point on the graph as shown below:

the least amount of fencing will be used when the length is equal to 31.62277766 and the width is equal to 15.8113883.
the area will be 500 square because 31.62277766 * 15.8113883 = 500.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!   = total length of fence (in yards), = total length of fence (in yards),  = area in square yards, = area in square yards,
 = length of each side of the fence directly attached to the building = length of each side of the fence directly attached to the building
If you are studying Calculus, you would want to use functions and derivatives to find the maximum of Area as a function of one of the measurements.
If you are not studying calculus, or learning how to use a graphing calculator, you need an easier solution:
The more common version of this type of problem, asks for the maximum area for a given total length of fence.
The general answer is that the best enclosure is always a double square,
meaning that the rectangular enclosure looks like two squares attached to the wall:

In other words, half of the length of the fence is the long side parallel to the building wall,
the other half is used for the two sections of fence that connect that long side to the wall.
To prove that, you would write that  --> --> , ,
and realize that  is a quadratic function that graphs as a parabola, is a quadratic function that graphs as a parabola,
and has a vertex/maximum for
 ---> ---> --> -->
That gives you the most efficient way to fence three sides of an enclosure,
yielding the maximum area for a given total length of fence:
 or or  . .
Obviously, 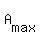 increases with increases with  (because (because 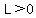 , of course). , of course).
So, if they just use  yards of fencing material, yards of fencing material,  , ,
the largest rectangular are you can enclose is  square yards: square yards:
 . .
They will need more fencing material.
If the parents use  yards of fencing material, yards of fencing material,  , ,
the largest rectangular are you can enclose is 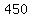 square yards: square yards:
 . .
They will need more fencing material.
What total length of fencing material will they need?
 ---> --->  ---> --->  <---> <---> . .
For an area of  square yards, they will need at least square yards, they will need at least
 yards of fencing material, yards of fencing material,
and the dimensions of the enclosure will be
  yards, yards,
and   yards. yards.
IF YOU ARE STUDYING CALCULUS:
You would write  as a function of some measure, as a function of some measure,
and calculate the derivative.
For example, if we were to use as a variable  , the length of the parallel fence sides, , the length of the parallel fence sides,
the length of the other side would be 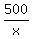 , ,
and the total length of fencing needed would be

The derivative of that functions is
 <--> <--> . .
That derivative is zero when  , for , for 
The derivative is negative (and the function decreases) for 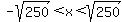 . .
For 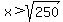 the derivative is positive and the function increases, the derivative is positive and the function increases,
so the function has a maximum for  , which is about , which is about 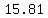 . .
That is the lengths of two of the sides of the fence.
The length of the other side of the fence is
 , which is about , which is about 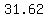 . .
|
|
|