Question 844469: A rectangle is inscribed fully inside an equilateral triangle. The triangle has a side length of 10. The rectangle shares one side with a triangle side (but the rectangle side is shorter than the triangle side. The rectangle's other two vertices each touch another side of the triangle.
I already know the entire triangle has an area of 25 radical 3. I would like to find the area of the rectangle. Or the area of the triangle excluding the rectangle.
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website! This may be difficult to follow without showing a diagram, figure, but think this way.
Cutting the triangle in half from one vertex to middle of the opposite side, you have a 30-60-90 triangle which you can fit onto a cartesian coordinate system. Putting the right angle at the origin, the triangle has vertices (0,0), (0,10), and (5,0). Equation for the line joining (0,10) and (5,0) is  .
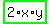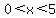Pick any (x,y) point on the line, and HALF of the rectangle in your description is x horizontally and y vertically. The area of your WHOLE rectangle will be  . That is two variables, and  and 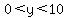 . Reminder, x here is equivalent from middle of the side of your equilateral to the endpoint of the rectangle's side.
We here have a formula for y, directly from the line in the graph I described. Area is  .
-
The actual rectangle's length horizontally will be 2x, and the tallness will be y. Pick your x, as long as it is 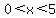and use the linear equation to find the corresponding y value. The area for the rectangle will be  .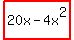
|
|
|
