Question 837626: I have a problem: For a world Peace day celebration the students at cabot high school are making a 6 m by 8 m flag. Each of the six grades will create a motif to honor the people of the six inhabited continets. Sketch three possible ways to divide the flag. One into six congruent triangles; one into sixs triangles with equal area but none congruent; and one into six congruent trapezoids. Give measuresments or makings on your sketches so each class knows it has equal area
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! These are the first ideas that came to my mind.
The possibilities are probably endless, but it is hard enough to draw these three.
Six congruent triangles:
 Six right triangles with legs measuring 2m and 8m.
Six congruent trapezoids:
 Six trapezoids with bases measuring 5m and 3m, and a 2m side perpendicular to the bases, for a 2m height.
Six triangles with equal area but none congruent:
(I would draw this on grid paper. I will draw a grid of 1m by 1m squares).
 The red lines divide the whole 8m by 6m rectangle (area=(8m)(6m)=48 square meters) into 6 triangles, each with an area of 8 square meters.
Triangle A is an isosceles triangle with an 8m base and a 2m height, not congruent to any of the other triangles.
You could say that non-congruent triangles B and C have the same base and height (a 2m base and an 8m height). They are obviously not congruent to any of the other triangles.
Triangle D is an isosceles triangle with base and height measuring 4 m.
Triangle E also has a base and a height measuring 4m,but it is not isosceles, and not congruent to any other triangle.
All those triangles have areas that can be calculated as 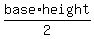 , and each has an area of 8 square meters:
Their areas add up to  square meters = square meters.
The remaining triangle (triangle F) must have an area of
48 square meters - 40 square meters = 8 square meters.
If the class assigned triangle F is not convinced enough, you could tell them that E and F together form a triangle with a 4m base and an 8m height, and that E+F triangle is divided into two equal parts by a median, the line segment between triangles E and F.
If they are still not convinced, they can use Heron's formula to calculate the area, using the lengths of the sides:
5m (for the side that is half a diagonal of the rectangle),  meters, and meters.
In that case, I would use the version that calculates the area as
 .
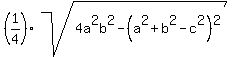(The letters  ,  and  are the side lengths).
|
|
|
