SOLUTION: how would i solve this type of question? If the ratio of the volumes of two similar geometrical solids is given by 121 : 36, and the surface area of the smaller solid is given b

Algebra ->  Surface-area -> SOLUTION: how would i solve this type of question? If the ratio of the volumes of two similar geometrical solids is given by 121 : 36, and the surface area of the smaller solid is given b      Log On


   

Question 824700: how would i solve this type of question?
If the ratio of the volumes of two similar geometrical solids is given by 121 : 36, and the surface area of the smaller solid is given by 1,200, what is the surface area of the larger solid?

Thanks for your time :)
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
Volume is measured in cubic units. The formulas to calculate volume all include a product which include three numbers which represent certain distances (length, width, height, radius, etc.). So even though we have no clue as to which type of solid is in this problem, we still know that its calculation involves the product of three lengths.

The problem also mentions that the two solids are similar, we know that the various corresponding lengths are proportional. This means the ratio of a length of one solid to the corresponding length in the other solid is the same for all pairs of corresponding lengths.

Putting this all together, the given ratio of the volumes, 121:36, is going to be the cube of the ratio of the corresponding lengths because there is the product three lengths in the volume. This makes the ratio of the lengths:
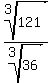
root%283%2C+121%29%2Froot%283%2C+36%29

Area (or surface area) is measured in square units. This means all area formulas include a product of two lengths. With similar logic as above, the ratio of the surface areas will be the square of the ratio of the lengths. So the ratio of the surface areas will be:
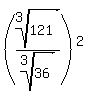
%28root%283%2C+121%29%2Froot%283%2C+36%29%29%5E2
which simplifies as follows:
%28root%283%2C+121%29%29%5E2%2F%28root%283%2C+36%29%29%5E2
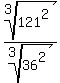
root%283%2C+121%5E2%29%2Froot%283%2C+36%5E2%29
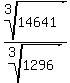
root%283%2C+14641%29%2Froot%283%2C+1296%29

Since we've been given the surface area of the smaller solid, we can now write a proportion which we can use to find the surface area of the larger solid. Using S for the surface area of the larger solid we get:
root%283%2C+14641%29%2Froot%283%2C+1296%29+=+S%2F1200
Multiplying by 1200 we get:
1200%2Aroot%283%2C+14641%29%2Froot%283%2C+1296%29+=+S
This is an exact expression for the solution and it may be acceptable as an answer. But it is not simplified or rationalized:
1200%2Aroot%283%2C+11%5E3+%2A+11%29%2Froot%283%2C+6%5E3+%2A+6%29+=+S

1200%2A%2811%2Aroot%283%2C+11%29%29%2F%286root%283%2C+6%29%29+=+S

1200%2A%2811%2Aroot%283%2C+396%29%29%2F%286root%283%2C+6%5E3%29%29+=+S
1200%2A%2811%2Aroot%283%2C+396%29%29%2F%286%2A6%29+=+S
1200%2A%2811%2Aroot%283%2C+396%29%29%2F36+=+S
A factor of 12 from the denominator cancels with the 1200:
100%2A%2811%2Aroot%283%2C+396%29%29%2F3+=+S
%281100%2Aroot%283%2C+396%29%29%2F3+=+S
This is an exact, simplified and rationalized expression for the solution. (Use your calculator if you want/need a decimal approximation for the solution. TO find the cube root on a calculator, raise 396 to the 1/3 power:
396^(1/3) [if your calculator has buttons for parentheses]
396^0.33333... [using as many 3's as possible in the exponent if your calculator does not have buttons for parentheses]