Question 818472: The rectangle has been broken into four smaller rectangles. The area of three
of the smaller rectangles are shown below. Find the area of the fourth one.
234
312
270
x
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! You must have a drawing to go with the problem.
Otherwise, there could be a lot of answers.
See NOTE 1 below.
If your drawing looks like this:
 and they do not tell you what area belongs to which rectangle. and they do not tell you what area belongs to which rectangle.
You know that one of the small rectangles (rectangle A in my drawing)
has the same width as a second small rectangle (B), and the same length as a third small rectangle (C).
If the width and length measures are whole numbers,
A could measure 18 by 13, with  , ,
B could measure 24 by 13, with  , and , and
C could measure 18 by 15, with  . .
In that case, the 4th small rectangle measures 24 by 15,
with are area of  . .
That is one possible solution.
How do we figure that?
Factoring.
The possible factorings for the areas are:
 , ,
 , and , and
 . .
No we look for common factors.
One of those area values is the area of rectangle A.
One of the factorings must have
one factor in common with the factoring for the area of B, and
the other factor in common with the factoring for the area of C.
We look for common factors, like  , ,
which appears in  and and  . .
Since we find  in in  , and , and
also as a factor of the third area value,  , ,
we know that the small rectangles could be as I described above,
a  by by  rectangle with area= rectangle with area=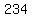 , adjacent to , adjacent to
a  by by  rectangle with area= rectangle with area=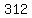 , and , and
a  by by  rectangle with area= rectangle with area= . .
However, it could also be that A is
 by by 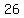 rectangle with area= rectangle with area=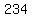 , adjacent to , adjacent to
a  by by  rectangle with area= rectangle with area= , and , and
a  by by 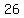 rectangle with area= rectangle with area=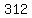 . .
That would make the 4th small rectangle
a  by by  rectangle with area= rectangle with area= . .
Or it could be that A is
 by by  rectangle with area= rectangle with area=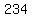 , adjacent to , adjacent to
a  by by  rectangle with area= rectangle with area= , and , and
a  by by  rectangle with area= rectangle with area=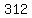 . .
That would make the 4th small rectangle
a  by by  rectangle with area= rectangle with area= . .
In all cases we end up with area= . .
We could prove why is that with a little algebra,
but maybe all that was expected is one possible set of dimensions and/or the result.
NOTE 1:
Let's say your drawing looks like this:
 and they do not tell you what area belongs to which rectangle. and they do not tell you what area belongs to which rectangle.
That is a different problem, and may have more than one solution.
At least you know that two of the smaller rectangles have the same width,
and that their lengths add up to the length of the large rectangle.
It could even be a more complicated picture, where none of the rectangles have obvious common dimensions.
I considered those possibilities, but my bet is that your problem is the one I solved above. If that's not the case, ask again.
NOTE 2:
When you post a problem, here or anywhere, try not to leave out important information, like a drawing that comes with the problem.
Also, when your problem is not answered here because it is too difficult, the child-geniuses in the forum of artofproblemsolving.com can solve it. Just do not expect a very detailed explanation, and do not "insult" them by posting a problem that is too easy for the level where you post it. For example, I would post this problem at the middle school level, or at the most basic high school level.
|
|
|