SOLUTION: please show me how to find the area of a regular hexagon with a perimeter of 100cm.

Click here to see ALL problems on Surface-area

Question 78947: please show me how to find the area of a regular hexagon with a perimeter of 100cm.
Found 3 solutions by stanbon, mathdoc314, Edwin McCravy:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website!
please show me how to find the area of a regular hexagon with a perimeter of 100cm.
----------------
Each side is 100/6 cm
Draw two consecutive line segments from the center
forming a triangle with the side.
The central angle is 360/6=60 degrees.
So the base angles are each 60 degrees also.
Draw the perpendicular bisector from the center
to the base. Each of the small triangles is a
60-30-90 rt triangle. The side opposite the
30 degree angle (half the side of the hexagon)
is half the hypotenuse. Knowing two of the sides
of the triangle you can find the altitude of the
60-60-60 triangle. You can now find the area
of the 60-60-60 triangel. Multiply that area
by six to get the area of the hexagon.
=============
Cheers,
Stan H.

Answer by mathdoc314(58)   (Show Source):
You can put this solution on YOUR website!
It would be easier to draw this, but here goes - I will type it

P ___ Q U /___\ R \___/ T S

Draw diagonals QT and PS too.
Label the center O.
This divides your regular hexagon into six equilateral triangles.
These lines all have equal length:
PQ, QR, RS, ST, TU,UP,PO,QO,RO,SO,TO,UO
The perimiter is 100 (all lengths in cm here) so if s is the length of those lines then 6 s = 100, or s = 100/6 (cm)

There is a point halfway between S and T on line ST (the midpoint).
Label this as M. Consider the triangle OSM:

O |\ h | \s | \ M ---- S s/2

Use the pythagorean theorem (or trig) to find out the missing height h:

Now you know the area of triangle OMS is
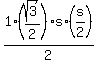(one half times the base times the height)
simplified,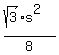
The area of the hexagon is 12 times this because the hexagon can be decomposed exactly into 12 triangles each congruent to OSM.

This is approximately 721.688
As a check, compare to the area of the circumscribed circle of the hexagon
pi * (100/6)^2 = 872.665
I would expect these two areas to be a little closer together. You may want to check my work above. But I think it is pretty much right.

Answer by Edwin McCravy(20055)   (Show Source):
You can put this solution on YOUR website!

please show me how to find the area of a regular hexagon with a perimeter of 100cm. ________ / \ / \ / \ \ / \ / \________/ Since the sum of all 6 sides is 100cm and since all the sides are equal, each one is 100/6 cm or 50/3 cm. The hexagon is made up of 6 equilateral tringles like this: _______ /\ /\ / \ / \ /____\ /____\ \ / \ / \ / \ / \/_____\/ So we will find the area of one of those equilateral triangles and then multiply it by 6. / \ 50/3/ \50/3 /_____\ 50/3 To find the area of that equilateral triangle we must find its height so we can plug in the formula for the area of a triangle: A = (base)(height)/2 To do that we draw in the height, hy /|\ 50/3/ |h\50/3 /__|__\ 50/3 To find that height, we notice that the height divides the equilateral triangle into two right triangles, and here is the left one: /| 50/3/ |h /__| where the bottom side is 1/2 of 50/3 or 25/3 /| 50/3/ |h /__| 25/3 Now we use the Pythagorean theorem to find h = = = = = = = Now we can find the area of the equilateral triangle /|\ 50/3/ |h\50/3 /__|__\ 50/3 A = (base)(height) A = A = A = and since the area of the regular hexagon is 6 of these, we multiply that by 6 and get5 Area of hexagon = Area of hexagon = Area of hexagon = Edwin