Question 785482: Two square pieces of equal dimensions made of thin cardboard are kept one on another in such a way that their sides and vertices coincide. The square piece on top is now rotated about its centre by an angle of 45 degrees. Find the ratio of the area covered by the pieces to the area of one of the square pieces.
• 2:1
• 11:18
• 1:2
• 11:9
• 18:11
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! This is what the two cardboard squares would look like after rotating one by  :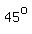
 The two pieces of cardboard cover an 8-point star shaped area.
I interpret the problem as asking for the ratio of the star area to the area of one square.
The key is finding the area of the 4 isosceles right triangles (star points) sticking out from under the square on the top.
I first thought that the problem was designed wrong, because the answer should involve irrational numbers, and could not be something as simple as 18:11, or any of the other choices given. I am starting to think that it is desgned to encourage you to make smart estimates for a quick answer that will gain you points in a multiple choice test. So I will give you two ways of solving it.
THE ESTIMATE WAY:
The ratios, in order of smaller to larger are
1:2, 11:18 (both less than 1:1), 11:9, 18:11, and 2:1
There is no "none od the above" option.
We have to pick one of the ratios given, so we need a smart estimate.
In a fast paced, high stakes, multiple choice test you can picture, or sketch the squares with the top one split into 9 equal square, like this:
 The 4 star-point triangles sticking out could be rearranged into 2 squares that would be like the blue and red small square in the corner, a little smaller than each of the 9 green squares.
If they were the same size, the area of the star would be 11 of the green squares compared to the 9 green squares forming the original large square. So the estimate is  . We know the real ratio is a little less than that, but it is certainly more than 1:1, and certainly less than 18:11.
If this was homework for a fifth grader could draw the square and the star on thin cardboard, cut out the shapes, and weigh them to get a good estimate of the ratio.
THE EXACT CALCULATION WAY:
I can make up my units of measure, and I say that the length of the side of the square is my unit of length.
 = side of one square (in units of my choice)
 = area of one square (in square units)
Now I define
 = leg of one of the right triangles sticking out
The hypotenuse of those triangles measures
 
The area of each triangle is
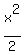
and the sum of the areas of all 4 triangles is
The area of the star is the area of the square plus the area of those 4 triangles,
SO the ratio of the area of the star ( to the ratio of the square is
(
That is not the same as  , but it is close.
|
|
|
