Additional info is needed for a numeric answer. Without knowing x or y or some other relation between them, the answer will contain at least one variable.
A = 1/2 a *P where a is apothem and P is perimeter.
1/2 * 1/2 y * 10x = 5xy/2: Answer 1.
You can go further by cutting the pentagon into 5 triangles, and cutting each of those into two right triangles with height 1/2 y and base x. The triangles thus formed are 36 (opposite the side length x), 54 (opposite the side length 1/2 y) 90 triangles.
Then tan(36) = x/(1/2y) so x = 1/2 y * tan(36)
Substitute that back into the 5xy/2 gives 5*(1/2 y *tan(36))*y /2 = 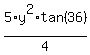 Answer 2.
Answer 2.
tan(54) = y/2x and 2x*tan(54) = y
Then 5xy/2 = 5x*2x*tan(54)/2 =  Answer 3.
Answer 3.
Those three answers are equivalent.
Hope the solution helped. Sometimes you need more than a solution. Contact fcabanski@hotmail.com for online, private tutoring, or personalized problem solving (quick for groups of problems.)