Question 647779: Bonnie Wolansky has 100ft of fencing material to enclose a rectangular exercise run for her dog. One side of the run will border her house,so she will only need to fence three sides. What dimensions will give the enclosure the maximum area? What is the maximum area?
Answer by Sarpi(32)   (Show Source): (Show Source):
You can put this solution on YOUR website! Material available = 100ft (the constraint)
Need a rectangle of only three sides - either 2 length with 1 breadth/width or 2 breadth/width with 1 length.
Let x = length and y = width denote the sides of the rectangle (assuming 2 length and 1 width)
=> The perimeter is  .... eqn 1 .... eqn 1
and the Area is  .................... eqn 2 .................... eqn 2
Then, we make y the subject in eqn1 to substitute into eqn2
eqn1 => 

 .....eqn3 .....eqn3
therefore, eqn3:  into eqn2: into eqn2:
=> 
= 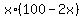 ....eqn4 ....eqn4
However, since eqn4: 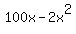 or or 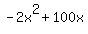 is an equation of a parabola curve, thus, we calculate the maximum point for x using the formula is an equation of a parabola curve, thus, we calculate the maximum point for x using the formula 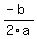
From the eqn4, a = -2 and b = 100
so, 
= 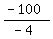
= 25 (hence, x, one side of rectangle (the length) is 25ft)
Given x = 25ft, we find the value for other side(y)
From eqn3: 


y = 50 (hence, y, the other side (the width) is 50ft)
The maximum area can be achieved with 2 sides = 25ft and 1 side = 50ft
Area = 
Area = 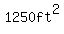
The graph of 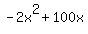

Hence, from the graph above, it can be clearly seen that the maximum point of the graph lies between 20 and 30 on the x-axis which is 25ft.
|
|
|