Question 643391: please help me verify which answer is correct#1 or #2 ?
A rectangular box with a square base is open at the top and has a volume of 12 cubic feet. Each side of the base has a length of x feet. Which of the following expresses the surface area, S,in square feet, of the outside of the box in terms of x ? (CLEP precalculus test)
#1:S=x^2+(48/x) or #2: S= x^2+(24/X)I got #2 but the answer key said #1 is correct answer. It didn't explain Why? please show me how to solve it. Thank you
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
please help me verify which answer is correct#1 or #2 ?
A rectangular box with a square base is open at the top and has a volume of 12 cubic feet. Each side of the base has a length of x feet. Which of the following expresses the surface area, S,in square feet, of the outside of the box in terms of x ? (CLEP precalculus test)
#1:S=x^2+(48/x) or #2: S= x^2+(24/X)I got #2 but the answer key said #1 is correct answer. It didn't explain Why? please show me how to solve it. Thank you
Since base = x, then area of base = 
Since volume of box = 12 cub. ft, and since Volume = LWH, then we can say that:
x(x)(H) = 12, with H being the height of the box
 ------ ------ 
 ------ ------ 
Since S, or surface area of the OPEN box = L*W (base, or bottom) + 2*L*H (front & rear) + 2*W*H (left and right sides), then we have:




 ----- Substituting ----- Substituting 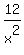 for H for H
 ---- Canceling x in numerator and denominator ---- Canceling x in numerator and denominator

Send comments and “thank-yous” to “D” at MathMadEzy@aol.com
|
|
|