Question 622471: A square prism in inscribed in a cylinder. The prism has a height of 12 inches and the cylinder has a radius of 5 inches. What's the lateral area and surface area of the prism and the cylinder
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I assume that from above you just see the bases of the prism and the cylinder, looking like a square inscribed in a circle, like this:
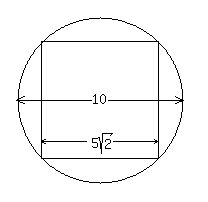 The diameter of the circle is 10 inches, the length of the diagonal of the square. The diameter of the circle is 10 inches, the length of the diagonal of the square.
Two sides of the square, of length x inches, form a right triangle with the diagonal for a hypotenuse, so
 --> -->  --> -->  --> --> 
The area of the circle (with radius 5) is  square inches. square inches.
That circle is one of the two congruent (equal) bases of the cylinder.
The circumference is  inches, and the lateral area of the cylinder is that times the height, or inches, and the lateral area of the cylinder is that times the height, or
 square inches. square inches.
So the total surface area of the cylinder is
 square inches. square inches.
The area of the square is  square inches. square inches.
That square is one of the two congruent (equal) bases of the prism.
The perimeter of the square is  inches, and the lateral area of the prism is that times the height, or inches, and the lateral area of the prism is that times the height, or
 square inches. square inches.
So the total surface area of the cylinder is
 square inches. square inches.
|
|
|