Question 192424: This is a practice problem for my daughter's upcoming state tests. We have a rectangular box measuring 12in. length, 8in. width and 3in. high. We calculated the volume to be 288 m3, and the surface area to be 312 m2. They are asking for us to find the dimensions of a box that has the same volume, but less surface area. How does she do this?
Thanks, Leslie
Found 2 solutions by stanbon, ankor@dixie-net.com:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! We have a rectangular box measuring 12in. length, 8in. width and 3in. high. We calculated the volume to be 288 m3, and the surface area to be 312 m2. They are asking for us to find the dimensions of a box that has the same volume, but less surface area. How does she do this?
-------------------
Consider a cube which has a side equal to cube root of 288.
---------
The volume will be 288 m^3 and the surfact area will be
6(cube root of 288)^2, which is less than 312 m^2
============================================================
Cheers,
Stan H.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! This is a practice problem for my daughter's upcoming state tests. We have a rectangular box measuring 12in. length, 8in. width and 3in. high. We calculated the volume to be 288 m3, and the surface area to be 312 m2. They are asking for us to find the dimensions of a box that has the same volume, but less surface area.
:
A square box gives max volume; let x = the 3 dimensions; then
x^3 = 288
x = 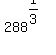 use a calc use a calc
x = 6.604 would be very close (6.604^3 = 288.02)
:
Find the surface area of this box:
SA = 2x^2 + 2x^2 + 2x^2
SA = 6x^2
SA = 6 * 6.604^2
SA = 261 sq in only
|
|
|