Question 1210563: help me understand how to calculate surface area of any prism
Answer by KMST(5338)   (Show Source): (Show Source):
You can put this solution on YOUR website! There are many shapes that can be called a prism. A box, like many of the ones that are delivered to my house, is a prism.
Most of those boxes have 6 faces, in 3 pairs of parallel faces.
You may think the face that is at the bottom is the base, because in everyday day language what we call base is something that is (or is supposed to be) at the bottom.
In math, it is different, and definitions are strict.
To be called a prism, a 3-dimensional shape needs to have flat (planar) faces, so a cylinder is not a prism because it has a curved surface.
Also, at least 2 of a prism's faces must be polygons of the same shape and size, and parallel to each other.
If there is more than one pair of parallel faces, we pick one, pair, and call those faces the bases of the prism.
The other faces connect one base to the other, forming what we could call the lateral surface.
To calculate the surface area of a prism, we calculate the surface area of each of the bases, and of each of the other faces, and we add them all up.
A see-through prism could look like this:
 That shape reminds me of a type of chocolate-based candy bar. That shape reminds me of a type of chocolate-based candy bar.
That prism has two triangular bases parallel to each other, and 3 rectangular sides not parallel to anything.
The triangular sides are called the bases of the prism, even if they were not at the bottom and top.
The faces of this prism look like this:  , two triangular bases and three rectangular sides that connect them. , two triangular bases and three rectangular sides that connect them.
Because the lengths of the sides of the triangular bases (3 cm and 3.4 cm) are not all the same, it is not a regular prism.
A prism is called a regular prism if the bases are regular polygons, with equal side length and equal angle measures.
A regular right prism is what is commonly shown in problems and examples.
Our prism is a good example of an "any prism" for the purpose of understanding surface area.
We can calculate the total surface area by adding the areas of the prism faces.
Because we have all the measures in centimeters, we calculate the surface areas in square centimeters  . .
A square centimeter is the amount of surface area in a square with sides measuring one centimeter.
How can we calculate how many square centimeters are in that rectangular side that is 3 cm wide and 7 cm long?
How many little square tiles with edges measuring 1 cm would it take to tile over that rectangle?
Three rows of 7 tiles amounts to 3x7=21 tiles.
The bottom rectangle's surface area is 
It is obvious that to calculate the area of a rectangle you just multiply length times width.
We do not need to memorize Area = L x w for a rectangle, because it's obvious, and we understand it.
Now we can calculate the areas of those 3 rectangles and add them up,
but how about if we calculated the area of a rectangle made of all 3 "glued" along their long sides?
That would make a rectangle with two side measuring 7cm,
and the other two measuring 
Instead of separately calculating the surface area of the three rectangular sides, we can calculate that way what in math we call the "lateral area" of the prism as
 , where , where 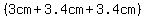 is the sum of the sides of the triangular base (the perimeter of a base), is the sum of the sides of the triangular base (the perimeter of a base),
and 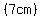 is the length of the rectangular sides and it is also the height of the prism. is the length of the rectangular sides and it is also the height of the prism.
If I placed one base of the prism horizontally, the rectangular sides would be vertical, and the bases would be one directly above the other, 7cm apart.
That makes it what we call a right prism, because it looks like it is standing upright rather than leaning to one side.
In math the distance between the parallel bases of a prism, measured perpendicular to those bases is called the height of the prism, regardless of the position of the prism.
Similarly, for all right prisms, regular, or not, lateral area = perimeter of the base X height of the prism.
To get the (total) surface area of a prism we have to add to the lateral area the areas of the bases, which is twice the area of a base because both have the same shape and size.
We can calculate the surface area of each of our prism's triangular bases as

Adding the lateral area, we can calculate the total surface area of our prism as

For other irregular right prisms the total area would be calculated similarly after figuring out how to calculate the area of each particular base shape, given the necessary base measurements.
For regular right prisms the surface area of the regular polygon bases can be calculated from the length of the polygon side based on the fact that all regular polygons with n-sides can be split into n equal triangular "pie slices".
For example, the area of a regular hexagon is the sum of the areas of 6 equilateral triangles:
 The height (a) of those equilateral triangles can be calculated as The height (a) of those equilateral triangles can be calculated as  times the length of the side, based on the Pythagorean theorem. times the length of the side, based on the Pythagorean theorem.
The area of each triangle would be  , and the area of the whole regular hexagon could be calculated as , and the area of the whole regular hexagon could be calculated as

All regular polygon areas can similarly calculated as  where where  can be calculated based on trigonometric ratios, or found tabulated for polygons with different numbers of sides. can be calculated based on trigonometric ratios, or found tabulated for polygons with different numbers of sides.
Oblique prisms are those with lateral surfaces not perpendicular to the bases, and the lateral sides are not necessarily rectangular.
To calculate their lateral areas you would not use the height of the prism, but calculating their surface areas is not commonly required.
|
|
|