SOLUTION: A regular hexagon is below. Solve for the area of the hexagon. https://ibb.co/dsnSzSLK A watch has the SAME hexagonal face as the picture to the left. If the radius of the circle

The area of any regular hexagon is six times the area of the central equilateral triangle.


In your case, the central equilateral triangle has the side length a = 14 units.


Its height is  h = .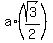


So, the area of the central equilateral triangle is  

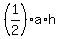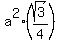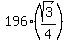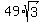     =  =  =  =  =   square units.


The area of the hexagon is then 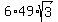  =  = 509.2229 square units (approximately).    ANSWER

To solve the second problem, from the area of the hexagon   = 509.2229 square units 
subtract the area of the circle   = 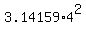 = 50.26544  square units.


You will get then

    the area of the shaded region = 509.2229 - 50.2644 = 458.9575 square units  (approximately).    ANSWER