SOLUTION: ABFE is a square. EBCD is a kite. Find the area of the composite figure. https://ibb.co/n8tynFcF

Algebra ->  Surface-area -> SOLUTION: ABFE is a square. EBCD is a kite. Find the area of the composite figure. https://ibb.co/n8tynFcF      Log On


   

Question 1210279: ABFE is a square. EBCD is a kite. Find the area of the composite figure.
https://ibb.co/n8tynFcF
Found 2 solutions by greenestamps, mccravyedwin:
Answer by greenestamps(13198) About Me  (Show Source):
You can put this solution on YOUR website!


EB is the diagonal of a square; its length is 12. Since AEB is an isosceles right triangle, the side length of the square is 12%2Fsqrt%282%29=6%2Asqrt%282%29.

AEB, FEB, and FBC are all congruent. Using the standard formula one-half base times height for the area of a triangle, the area of each of those triangles is

%281%2F2%29%286sqrt%282%29%29%5E2=%281%2F2%29%2872%29=36

Note some students will find it easier to view each of those three triangles as one-quarter of a square with side length 12, making the area of each one

%281%2F4%29%2812%5E2%29=144%2F4=36

Either way, the area of ABCE is 3*36 = 108.

Angle EDF is 30 degrees, so triangle EDF is a 30-60-90 right triangle with a short leg of length 6%2Asqrt%282%29. Using the properties of a 30-60-90 right triangle, the length of DF is

%286sqrt%282%29%29%28sqrt%283%29%29=6sqrt%286%29

DF is the altitude of triangle CDE.

Then the area of triangle CDE -- again using the standard formula one-half base time height -- is

%286sqrt%282%29%29%286sqrt%286%29%29=36sqrt%2812%29=72sqrt%283%29

And so the area of the composite figure is

ANSWER: 108%2B72sqrt%283%29

Answer by mccravyedwin(406) About Me  (Show Source):
You can put this solution on YOUR website!

I've been tutoring a high school kid in geometry recently, and discovered 
that these days, schools are really stressing special right triangles, using
ratio and proportion between the "standard" special right triangles, and the
right triangles they are given.  So I will use that approach entirely.  



The figure is composed of 
three 45-45-90 congruent right triangles, BAE, BFE, and BFC.
and
two 30-60-90 congruent right triangles, DFE and DFC

Each 45-45-90 right triangle has hypotenuse 12.

We set up a ratio between the "standard" 45-45-90 right triangle and
the given 45-45-90 right triangle, letting the leg be x:



hypotenuse%2Fleg=hypotenuse%2Fleg
12%2Fx=sqrt%282%29%2F1
12=x%2Asqrt%282%29


So the area of each 45-45-90 right triangle is 



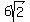Each 30-60-90 right triangle has shorter leg 6sqrt%282%29

We set up a ratio between the standard 30-60-90 right triangle and
your 30-60-90 right triangles, letting the longer leg be x:




%28x%29%2F%286sqrt%282%29%29=sqrt%283%29%2F1
x=6sqrt%282%29%2Asqrt%283%29=6%2Asqrt%286%29



Since the figure is composed of three 45-45-90 congruent right triangles, and
two 30-60-90 congruent right triangles,

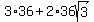The area of the composite figure is 3%2A36%2B2%2A36sqrt%283%29

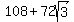or 108%2B72sqrt%283%29

Edwin