Question 1199419: In the diagram, line BC = 5 cm, and curved line DE is tangent to line AC. Find the area, in cm2, of the quarter circle BDE with centre B.
https://ibb.co/6bcN9jh
A) 160
B) 215
C) 245
D) 260
E) 280
Found 5 solutions by josgarithmetic, ikleyn, math_tutor2020, MarkSingh-, MathTherapy:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! Just a very small piece of help:
Notice the triangle is special 30-60-90 type. Length BA AC is 10 cm.
Also, if you draw a segment from point B to the tangency point, you cut the triangle into two similar triangles. You may remember or find a rule which gives some information about this.
If you use these and setup a proportion for the circle's radius, r, ....
you may find  . .
(Rationalize if you feel you want to.)
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How you formulate the problem in your post, it makes me cry:
so mathematically illiterate the formulation is.
Therefore, I will edit it to present it in a decent shape.
In the diagram, ABC is a right triangle with the right angle at B.
Angle C is 30°. The leg BC is 5 cm long.
Circular arc DE with the center at B is tangent to hypotenuse AC.
Find the area, in cm2, of the quarter circle BDE.
Next, the solution by @josgarithmetic is incorrect,
starting from the second line of his post.
AB is not 10 cm, as he mistakenly states in his post.
Therefore, ignore his solution, since it is wrong.
I came to bring you a correct solution.
Since the angle A is 30°, the hypotenuse AC is 10 cm and the leg AB is 10*cos(30°) = 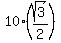 = = 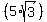 .
Then the area of the triangle ABC is .
Then the area of the triangle ABC is  = = 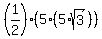 = = 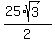 .
Next, the radius of the circle "r" is the height of the triangle ABC, drawn from vertex B to the hypotenuse AC.
Therefore, the area of the triangle ABC in other form can be presented as .
Next, the radius of the circle "r" is the height of the triangle ABC, drawn from vertex B to the hypotenuse AC.
Therefore, the area of the triangle ABC in other form can be presented as 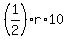 cm^2.
The area is the same, so we can write this equation cm^2.
The area is the same, so we can write this equation
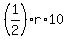 = = 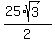 cm^2.
It gives
r = cm^2.
It gives
r =  cm.
Now the area of the quarter of the circle is cm.
Now the area of the quarter of the circle is
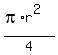 = = 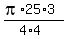 = = 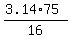 = 14.72 cm^2 (rounded). ANSWER = 14.72 cm^2 (rounded). ANSWER
Solved.
---------------------
No one of the listed numbers in your post is not even close to the right answer.
It is easy to see, without making long calculations, that all listed numbers in your post are not even close to the right answer.
Indeed, the radius of the circle is, obviously, shorter than 5 cm.
Hence, the area of the quarter of the circle MUST be less than 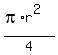 = = 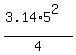 = 19.625 cm^2. = 19.625 cm^2.
Compare it with your numbers.
Then REPORT to YOUR PROFESSOR that all your
attached answers ARE INCORRECT NUMBERS.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The tutor @ikleyn has the right idea.
However, she made a slight typo.
Side AB should be 5*sqrt(3) cm long.
Edit: Ignore this paragraph as she has corrected the error.
For any 30-60-90 triangle, we have this template
short leg = x
long leg = x*sqrt(3)
hypotenuse = 2x
In this case x = 5
The short leg of this template is always opposite the 30 degree angle.
Smallest side opposite the smallest angle.
Since AB = 5*sqrt(3) and BC = 5, it leads to triangle ABC having an area of (25/2)*sqrt(3) square cm.
I skipped the steps so let me know if you need to see them.
Then solving the equation
(1/2)*r*10 = (25/2)*sqrt(3)
will lead to
r = (5/2)*sqrt(3)
area of the full circle = pi*r^2
area of quarter circle = (1/4)*pi*r^2
area of quarter circle = (1/4)*pi*( (5/2)*sqrt(3) )^2
area of quarter circle = (75/16)pi
area of quarter circle = 4.6875pi
area of quarter circle = 4.6875*3.14
area of quarter circle = 14.71875
The value is approximate because pi = 3.14 is approximate.
Unfortunately none of the answer choices you posted are close to this value.
It's possible your teacher made a typo, or you might have mixed up problems/answer choices by mistake.
Please revise carefully.
Answer by MarkSingh-(4)   (Show Source): (Show Source):
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
In the diagram, line BC = 5 cm, and curved line curve DE is tangent to line AC. Find the area, in cm2, of the quarter circle BDE with centre B.
https://ibb.co/6bcN9jh
A) 160
B) 215
C) 245
D) 260
E) 280
 .
Draw BF, a radius of quarter-circle BDE, to AC at the point where the tangent touches the quarter-circle. Notice that the tangent
line AC, and the radius BF form a right angle (A right angle is formed at the point of tangency of a circle, with its radius)
With BF being r, we now see a right triangle, BFC, with ∡BFC being 90o.
Additionally, ∡BCF = 60o, which then creates a 30-60-90 SPECIAL ▲, in BFC.
With special right ▲BFC having hypotenuse BC measuring 5 cm, ∡BCF measuring 60o, its longer leg BF, a radius of quarter-circle BDE,
would be .
Draw BF, a radius of quarter-circle BDE, to AC at the point where the tangent touches the quarter-circle. Notice that the tangent
line AC, and the radius BF form a right angle (A right angle is formed at the point of tangency of a circle, with its radius)
With BF being r, we now see a right triangle, BFC, with ∡BFC being 90o.
Additionally, ∡BCF = 60o, which then creates a 30-60-90 SPECIAL ▲, in BFC.
With special right ▲BFC having hypotenuse BC measuring 5 cm, ∡BCF measuring 60o, its longer leg BF, a radius of quarter-circle BDE,
would be  We then get: area of quarter-circle
We then get: area of quarter-circle  NONE of the answer choices are even close to that!
It would NOT behoove me to speculate why!
NONE of the answer choices are even close to that!
It would NOT behoove me to speculate why!
|
|
|