I'm not sure what you want here. But I'll do enough of it to get you
so you can finish.
Let AB be the chord which divides the area of the circle so that
the area above AB is 1/3 of the area of the circle  .
Then the area below AB will be 2/3 of the area of the circle. Then
they will be in the ratio 1:2
.
Then the area below AB will be 2/3 of the area of the circle. Then
they will be in the ratio 1:2
 We draw in two radii to A and B.
We draw in two radii to A and B.
 First we find the area of the sector AOB ("piece of pie")
First we find the area of the sector AOB ("piece of pie")


 In this case,
In this case, 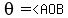


 We must subtract the area of triangle AOB to get the area
above AB.
If a triangle has two sides with lengths x and y, and the
angle between these two sides is θ degrees, then the area
of the triangle is given by the equation
We must subtract the area of triangle AOB to get the area
above AB.
If a triangle has two sides with lengths x and y, and the
angle between these two sides is θ degrees, then the area
of the triangle is given by the equation


 In this case, x and y both equal the radius r, and
In this case, x and y both equal the radius r, and 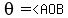


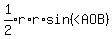


 The area above AB is
The area above AB is


 This must equal 1/3 of the area, which is
This must equal 1/3 of the area, which is 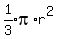 So the equation is
So the equation is




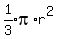 We divide through by r2
We divide through by r2




 You can only solve that for
You can only solve that for  with technology.
I used a TI-84 Plus. I got 149.27417o
Use that to find whatever else your teacher wants.
Edwin
with technology.
I used a TI-84 Plus. I got 149.27417o
Use that to find whatever else your teacher wants.
Edwin