SOLUTION: water flows into a tank havingthe form of frustum of a right circular cone. The tank is 4m tall with upper radius of 1.5 m and the lower radius of 1 m.when the water in the tank is

Click here to see ALL problems on Surface-area

Question 1188936: water flows into a tank havingthe form of frustum of a right circular cone. The tank is 4m tall with upper radius of 1.5 m and the lower radius of 1 m.when the water in the tank is 1.2 m deep the surface rises at the rate of 0.012 m/s . Calculate the discharge of water flowing into the tank in m3/s.
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website!
Here's how to calculate the discharge of water flowing into the tank:
**1. Find the radius of the water surface:**
* We can use similar triangles to relate the radius of the water surface (r) to the depth of the water (h).
* The ratio of the radii is equal to the ratio of the heights:
(r - 1) / (1.5 - 1) = h / 4
r - 1 = 0.5h / 4
r = 1 + 0.125h
* When h = 1.2 m:
r = 1 + 0.125 * 1.2 = 1.15 m
**2. Calculate the cross-sectional area of the water surface:**
* A = πr²
* A = π * (1.15)² ≈ 4.1548 m²
**3. Calculate the discharge (dV/dt):**
* The discharge is the rate of change of volume (dV/dt), which is equal to the cross-sectional area (A) times the rate of change of the water depth (dh/dt).
* dV/dt = A * dh/dt
* dV/dt = 4.1548 m² * 0.012 m/s
* dV/dt ≈ 0.049857 m³/s
**Answer:**
The discharge of water flowing into the tank is approximately 0.049857 m³/s.

Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.
Water flows into a tank having the form of frustum of a right circular cone. The tank is 4 m tall with upper radius of 1.5 m
and the lower radius of 1 m. When the water in the tank is 1.2 m deep, the surface rises at the rate of 0.012 m/s.
Calculate the discharge of water flowing into the tank in m3/s.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

        I will give a solution here different from that in the post by @CPhill.
        . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Here's how to calculate the discharge of water flowing into the conical frustum tank step by step.

                The geometry connections

We have the great cone with the base radius of 1.5 m and the height H m (H is measured from the vertex). We have the small cone with the base radius of 1 m and the height (H-4) m. This cone is cut out. Therefore, for the small cone we have this proportion from similarity = 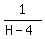, which gives 1.5H- 1.5*4 = H, 1.5H - H = 6, 0.5H = 6, H = 6/0.5 = 12. So, the great cone has the height H = 12 m; the small cone has the height 12-4 = 8 m, and for every current h from vertex and r we have 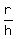= = 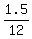= 0.125. Therefore, for any current h and r, r = 0.125h, where h is measured from the vertex. In particular, when r = 1 m (the lower radius), h = 12-4 = 8 meters from the cone vertex. When the height of the water in the tank is 1.2 meters, h = 8 + 1.2 = 9.2 meters and r = 0.125*(8+1.2) = 1.15 m.

                The volume of the water in the tank

When the level of the water is h meters from the vertex, the volume of the water is V = 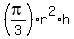- 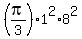m^3. Substituting here r = 0.125h, we have this formula for the volume of the water in the tank V = 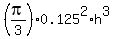- 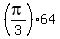m^3. We can consider here V and h as functions of time V(t) = - 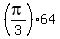m^3. (1)

                Differentiate the volume of the water in the tank

Write the derivative of the volume of the water in the tank in respect to the time. The constant term in formula (1) does not matter, so forget about it. 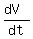= , Apply it for h = 8+1.2 = 9.2 meters. It will give 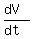= = 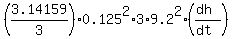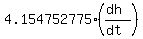Now substitute the given value of the rate of the surface rise 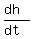= 0.012 m/s. You will get this equation 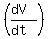= = 0.049857 (rounded). ANSWER. The inflow rate into the tank is about 0.049857 m^3/s.

Solved.