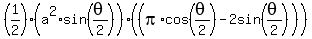Refer to the figure above, where we've sliced the original picture down the middle. Here  . If we maximize this figure in terms of
. If we maximize this figure in terms of  , we just need to double that to find
, we just need to double that to find  .
.
 =
= 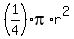
 =
= 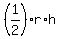
Observe:


Substituting for r and h:
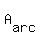 =
= 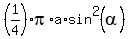
 =
= 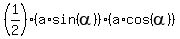
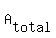 =
= 
= 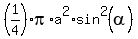 +
+ 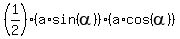
...factoring out 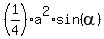
= 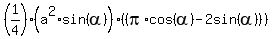 (*)
(*)
Now take the derivative of 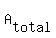 with respect to
with respect to 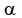 :
:
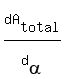 =
=
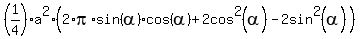
= 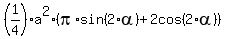
... substitute  ...
...
= 
This last function is zero at approx. 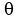 = 2.575rad,
= 2.575rad,  = 5.716rad, ...
= 5.716rad, ...
By graphing, one can see 2.575rad results in a maximum area, while 5.716 results in a minimal area.
2.575rad is approx 147.54degrees.
Ans:  =
= 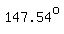 maximizes the total area.
maximizes the total area.
Just in case...
If you were interested in the value of the total maximal area, note that you would need a modified form of (*) because that equation computes 1/2 of the total area:
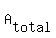 =
=