SOLUTION: When Fidel and Janette were married, his age was 3/2 of her age. If on their golden wedding anniversary, Fidel’s age will be 8/7 of Janette’s age, how old will each of them

Algebra ->  Surface-area -> SOLUTION: When Fidel and Janette were married, his age was 3/2 of her age. If on their golden wedding anniversary, Fidel’s age will be 8/7 of Janette’s age, how old will each of them      Log On


   

Question 1184989: When Fidel and Janette were married, his age was 3/2 of her age. If on their
golden wedding anniversary, Fidel’s age will be 8/7 of Janette’s age, how old will
each of them be on their golden anniversary?
Found 3 solutions by ikleyn, JBnovelwriter, MathTherapy:
Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
When Fidel and Janette were married, his age was 3/2 of her age. If on their
golden wedding anniversary, Fidel’s age will be 8/7 of Janette’s age, how old will
each of them be on their golden anniversary?
~~~~~~~~~~~~~~~~ 

Let x be the Janette age at the wedding year.

Then the Fidel's age was  %283%2F2%29%2Ax at this year.


On their golden wedding anniversary, the Janette age will be (x+50) years, while the Fidel's age will be %283%2F2%29%2Ax%2B+50.


We have this equation then


    %283%2F2%29%2Ax%2B50 = %288%2F7%29%2A%28x%2B50%29.


To solve it, first multiply both sides by GCD of 14; then simplify


    3*7*x + 700 = 2*8*(x+50)

     21x  + 700 = 16x + 800

     21x - 16x  = 800 - 700

        5x      =    100

         x      =    100/5 = 20.


ANSWER.  At marriage, Janette was 20 years old;  Fidel was  %283%2F2%29%2A20 = 30 years old.

Solved.



Answer by JBnovelwriter(34) About Me  (Show Source):
You can put this solution on YOUR website!
golden wedding happens at 50 years of marriage
F and J will be the variables
F=%288%2F7%29J
%28F-50%29=%283%2F2%29%28J-50%29
use substitution to solve.
%28F-50%29=%283%2F2%29%28J-50%29
%288%2F7%29J-50=%283%2F2%29%28J-50%29 multiply in
%288J%2F7%29-50=%283J%2F2%29-%28150%2F2%29simplify then add 50 to both sides
%288J%2F7%29=%283J%2F2%29-25 subtract 3j/2 from both sides
%288J%2F7%29-%283J%2F2%29=-25 multiply by a 1 to make the common denom 14
%282%2F2%29%288J%2F7%29-%287%2F7%29%283J%2F2%29=-25 multiply across for each one
%2816J%2F14%29-%2821J%2F14%29=-25subtract then multiply both sides by -1
%285J%2F14%29=25multiply both sides by 14
5J=350 divide
highlight%28J=70%29 50 years ago she was 20
F=%288%2F7%29J
F=%288%2870%29%2F7%29
highlight%28F=80%29 50 years ago he was 30
Make sure u note the answer the question wants is: "How old will
each of them be on their golden anniversary?"
It doesn't ask for what age they were when they got married. the other tutor seemed to have missed that part.

Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!

When Fidel and Janette were married, his age was 3/2 of her age. If on their
golden wedding anniversary, Fidel’s age will be 8/7 of Janette’s age, how old will
each of them be on their golden anniversary?
Let Janette's age, on their wedding day, be J
Then Fidel's, on their wedding day was: matrix%281%2C5%2C+3%2F2%2C+of%2C+J%2C+or%2C+3J%2F2%29
Janette's age, on their golden anniversary, will be: J + 50 
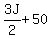Fidel's age, on their golden anniversary, will be: 3J%2F2+%2B+50
We then get: matrix%281%2C3%2C+3J%2F2+%2B+50%2C+%22=%22%2C+%288%2F7%29%28J+%2B+50%29%29
21J + 700 = 2(8)(J + 50) ------ Multiplying by LCD, 14
21J + 700 = 16J + 800
21J - 16J = 800 - 700
5J = 100
Janette's age, on their wedding day, or: highlight_green%28matrix%281%2C5%2C+%22J%2C%22%2C+was%2C+100%2F5%2C+%22=%22%2C+20%29%29
Fidel's age, on their wedding day, was: highlight_green%28matrix%281%2C3%2C+3%2820%29%2F2%2C+%22=%22%2C+30%29%29
You now can easily find their ages on their golden anniversary.