Question 1183787: Show that in the plane R^2, the area K of the parallelogram OXZY with vertices at O(0,0), X(x1,x2), Y(y1,y2), and Z(z1,z2) is given by
1. K^2 = |X|^2|Y|^2 - (X*Y)^2.
2. K = |x1*y2 - x2*y1|
Answer by robertb(5830)   (Show Source):
You can put this solution on YOUR website! 1. From vector calculus we know that 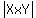 gives the area of the parallelogram spanned by the vectors  and  , and 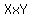 is their cross-product.
But  , where 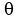 is the angle between the two vectors.
===> 
2. If Z= ( , ) is the diagonal vector of the parallelogram, then (,) = ( ,  ).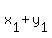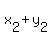
The area of the triangle bounded by X, Y, and Z is given by  ,
if direction of evaluation is done counter-clockwise. If the evaluation is done in clockwise manner, area is negative of the preceding value.
Hence, area of triangle is given by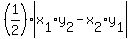 
But since the triangle mentioned above is half of the parallelogram, we then have  .
|
|
|
