SOLUTION: The diagonals of right trapezoid are perpendicular. What is the area of the trapezoid if the parallel bases measure 8cm and 18cm?

Make a sketch.


Let d be the shorter diagonal and D be the longer diagonal of the trapezoid.

Let H be the altitude of the trapezoid.


Then from Pythagoras, you have these two equations


    8^2  + H^2 = d^2      (1)

    18^2 + H^2 = D^2      (2)



Since the diagonals are perpendicular, there is this formula for the trapezoid area A

    A = 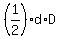.        (3)


From the other side, there is a classic formula for the trapezoid area as  

    A = 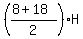      (4)


Equating (3) and (4), you have

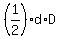     = 13H,   

or

    d*D = 26H.                  (5)



Thus we have three equations  (1), (2) and (5)  for three unknowns  d, D and H.

Now the most interesting part of the solution is starting.



Multiply equations (1) and (2).  You will get

    (64 + H^2)*(324 + H^2) = (d*D)^2.      (6)


Replace  (d*D)^2  in the right side of the equation (6)  by  (26*H)^2, based on (5).

By doing this way, you reduce the system of three equations in three unknowns (1), (2) and (5) 
to one single equation for H^2

    (64 + H^2)*(324 + H^2) = 676*H^2.


Simplify and solve (it is biquadratic equation for H)

    64*324 + 324H^2 + 64H^2 + H^4 = 676H^2

    H^4 - 288H^2 + 20736 = 0


Factor left side

    (H^2-144)^2 = 0.


It gives  H^2 = 144;  hence,  H =  = 12.


Thus we found that the altitude of the trapezoid H  is 12 cm.


Now the area of the trapezoid is 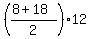  = 13*12 = 156 square centimeters.    ANSWER